Lesson (3): The relation between the inscribed angles subtended by the same arc

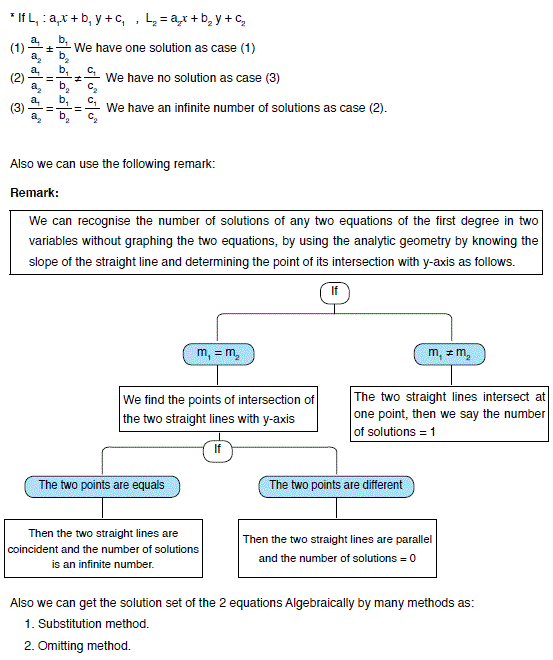
Lesson 1 : Solving 2 equations of 1st degree in two variables

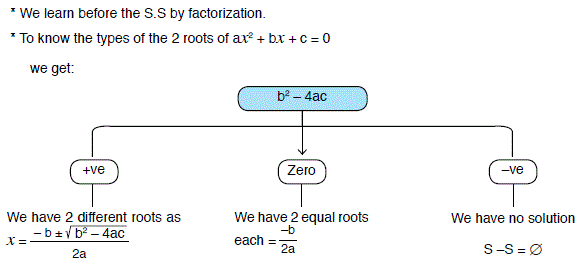
Lesson (2): Solving an equation of 2nd degree in one unknown (Graphically and Algebraically)

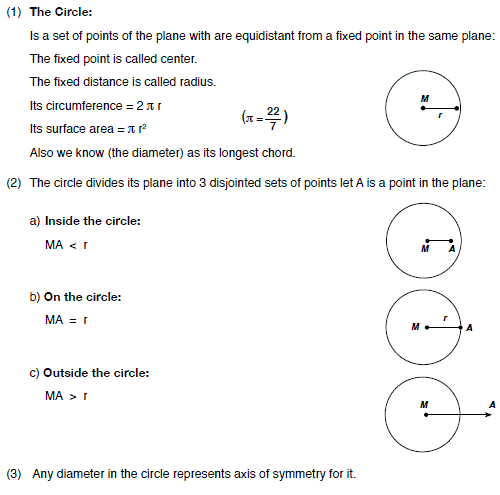
Lesson (1): Set of zeros of a polynomial function:

lesson (2) algebraic fractional function

Lesson (3) Equality of 2 algebraic fraction

Lesson (4) Operations on algebraic fractions

Lessons (1) , (2):

Lessons (1, 2)

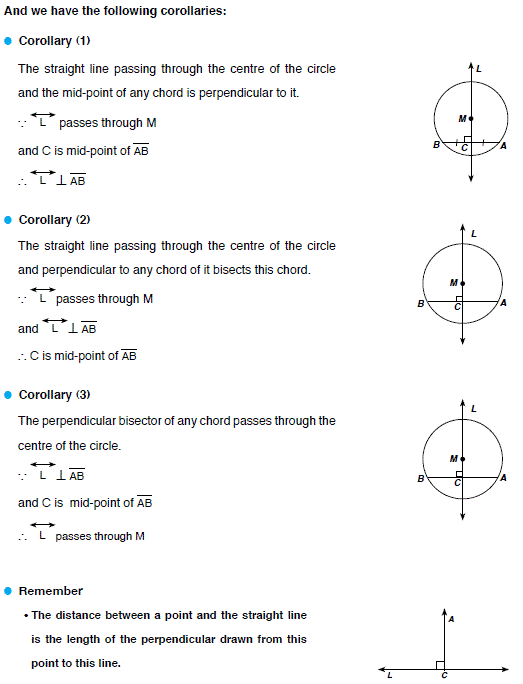
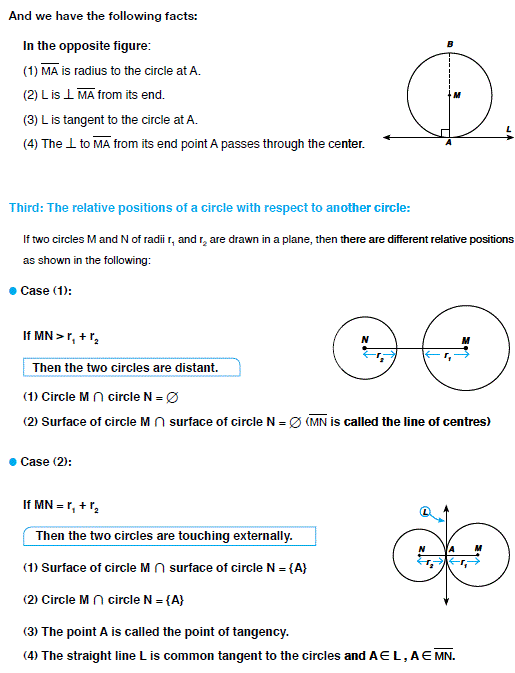
Lesson (3).

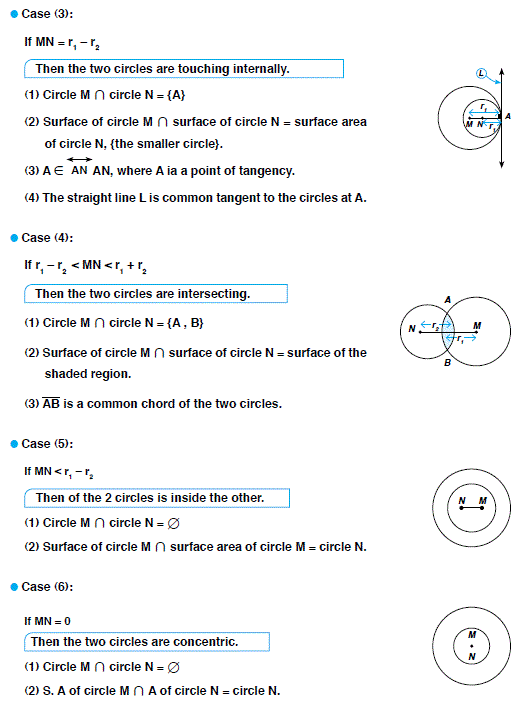
Lesson (4)

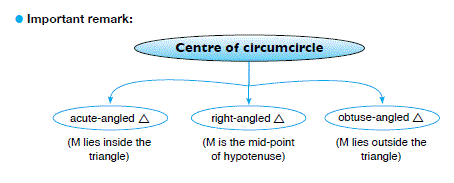
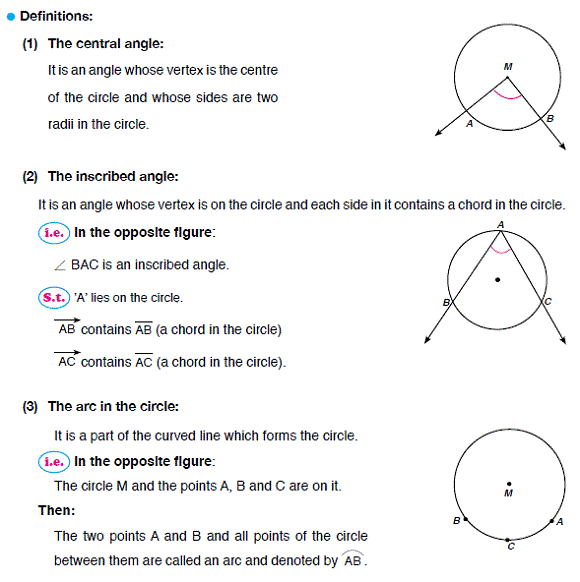
Lesson (1): Angles and arcs in the circle (central angles and measuring arcs)

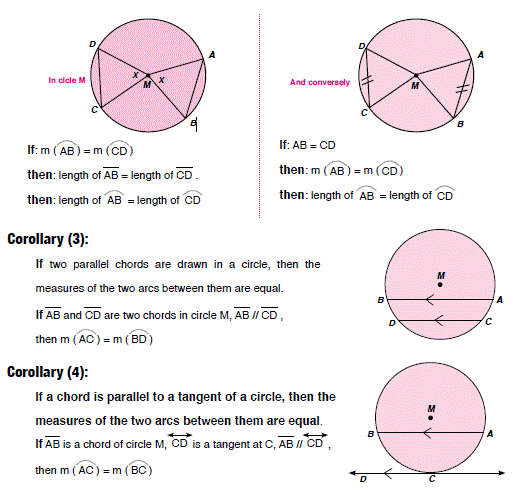
Lesson (2): The relation between the inscribed angle and central angle subtended to the same arc

Lesson (3): The relation between the inscribed angles subtended by the same arc

Lessons (4, 5)

* we define cyclic quad. as
Any quadrilateral figure in which its four vertices belong to acircle.
And it has the following properties:
(1) There exists a point in the plane which is equidistant from its vertices, this point is
the center of its circum-circle.
(2) Any 2 angles drawn on the same base and at one side from it are equal in measure.
(3) Any 2 opposite angles are supplementary.
(4) The measure of the exterior angle at one vertex is equal to the measure of the interior angle at the opposite of this vertex.
* If the quadrilateral is cyclic, all properties are satisfied.
* The converse is right, if we can prove any of the previous properties then the figure becomes cyclic.
* See theorem 3 and its converse with several cases in Al Adwaa Book Unit (5).
And we need to remember:
A quadrilateral is cyclic if there exist(s) one of the following:
(1) A point in the same plane equidistant from its four vertices.
(2) Two angles equal in measure drawn on one of its sides as a base.
(3) Two opposite angles being supplementary.
(4) An exterior angle at one of its vertices equals in measure the interior angle opposite to this vertex.
(5) If it's drawn inside a circle passing by its vertices.

lesson 7: the angle of tangency

Date: 2015-01-12; view: 1719