
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Base number of stress cycles
| BHNm | up to 200 | ||||||||
| HRCm | - | ||||||||
| NH0·106 | 16.5 | 36.4 |
2.3.3. Determine the service life in hours for the gearing:
t = L · 365 · Ka · 24 · Kd,
where L is the service life in years; Ka is the annual utilization factor that takes into account use of the gearing during year; Kd is the daily utilization factor that takes into account use of the gearing for 24 hours. These parameters should be given in the specification for the course paper.
2.3.4. Determine the factor KHE that reduces variable load conditions to the constant load equivalence.
KHE = 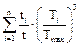 ,
,
where Tmax and Ti are correspondingly maximum and acting torques; ti is the time of action of the torque Ti.
If the time of action of the torque is less than 0.03·t this torque should not be taken into account.
2.3.5. Determine the equivalent number of cycles for the pinion and the gear.
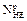 = 60×np×c×t×KHE ,
= 60×np×c×t×KHE ,
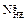 = 60×ng×c×t×KHE ,
= 60×ng×c×t×KHE ,
where np and ng are correspondingly rotational speeds of the pinion and the gear; c is the number of gears meshing with the gear being analyzed. In our case c=1.
2.3.6. Determine the durability factor for the pinion and for the gear.
if NHE ≥ NHO then KHL=1,
if NHE < NHO then KHL= 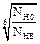 .
.
2.3.7. Determine the safety factor SH for the pinion and for the gear.
- for homogeneous structure of the material
(heat treatment is normalizing, martempering and full hardening) SH = 1.1;
- for heterogeneous structure of the material
(heat treatment is surface hardening, case hardening, nitriding) SH=1.2.
2.3.8. Determine the contact allowable stresses for the gear and for the pinion
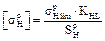 ,
, 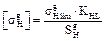 .
.
If Hp-Hg  70BHN we assume as the design allowable contact stress the less magnitude of above calculated stresses, where Hp and Hg are correspondingly hardness of the pinion and gear materials.
70BHN we assume as the design allowable contact stress the less magnitude of above calculated stresses, where Hp and Hg are correspondingly hardness of the pinion and gear materials.
Otherwise, the design allowable contact stress is determined by the following formula
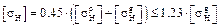 .
.
2.4. Determine the allowable bending stresses of the pinion and for the gear.
2.4.1 . Determine the limits of the bending endurance for the pinion 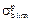 and for the gear
and for the gear 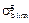 . For this purpose we use table 2.1.
. For this purpose we use table 2.1.
2.4.2. Determine the base number of stress cycles 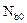 .
.
For steels 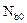 = 4∙106.
= 4∙106.
2.4.3. Determine the factor KbE that reduces variable load conditions to the constant load equivalence.
KbE = 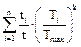 ,
,
where k=3 for toothed wheels with hardness H ≤ 350 BHN . If H > 350 BHN k=9.
2.4.4. Determine the equivalent number of cycles for the pinion and the gear.
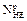 = 60×np×c×t×KbE ,
= 60×np×c×t×KbE ,
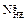 = 60×ng×c×t×KbE .
= 60×ng×c×t×KbE .
2.4.5. Determine the durability factor for the pinion and for the gear.
if NbE ≥ NbO then KbL=1,
if NbE < NbO then KbL= 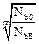 ,
,
where m=3 for toothed wheels with hardness H ≤ 350 BHN and m=9 if H > 350 BHN.
2.4.6. Determine the safety factor Sb for the pinion and for the gear.
- for wheels made of forged blanks (our case) Sb = 1.75;
- for wheels made of cast blanks Sb = 2.3.
2.4.7. Determine the bending allowable stresses for the gear and for the pinion
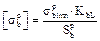 ,
, 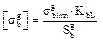 .
.
For further calculations we assume as the design allowable bending stress the less magnitude of above calculated stresses.
Date: 2014-12-22; view: 1745
| <== previous page | | | next page ==> |
| Table 2.1 | | | CLASSIFICATION OF UNCOUNTABLE NOUNS |