
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Compiling Equations of Oxidation-Reduction Reactions
In previous section, we considered very simple example of redox reaction - the formation of a compound from two elementary substances. Usually, the equations of redox reactions are more complicated and it is often quite difficult task to balance them. We shall consider a few examples.
Example 1. The reaction between Hydrogen Iodide and concentrated Sulfuric acid. This reaction proceeds as follows:
HI + H2SO4 (conc) → I2 + H2S + H2O.
If we calculate the oxidation number of each element in the reactants and in the products, we shall see that it changes both in Iodine and in Sulfur. In the Iodine of HI it is -1, and in free Iodine it is 0. The oxidation number of Sulfur, on the other hand, changes from +6 (in H2SO4) to -2 (in H2S). Hence, the oxidation number of Iodine increases, and of Sulfur decreases. Consequently, Iodine is oxidized, and Sulfur is reduced.
The equation of Iodine oxidation has a simple form:
2I- = I2 + 2 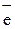 (oxidation)
(oxidation)
The equation of Sulfur reduction is more complicated because both the reactant (H2SO4 or SO42-) and the product (H2S) contain other elements in addition to Sulfur. In compiling this equation, we shall proceed from the fact that the reaction takes place in an acidic aqueous solution, and the ion SO42- transforms into the molecule H2S:
SO42- ® H2S.
The four Oxygen atoms liberated in this process should be combined with Hydrogen into four molecules of water. Eight Hydrogen ions are needed for this. In addition, two Hydrogen ions are needed to form a molecule of H2S. Hence, ten Hydrogen ions should react with the SO42- ion:
SO42- + 10 H+ ®H2S + 4H2O.
The total charge on the ions in the left-hand side of this formula is eight elementary positive charges, while the right-hand side contains only uncharged particles. Since the total charge does not change in the course of the process, eight electrons also participate in the reduction process:
SO42- + 10H+ + 8 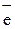 ® H2S + 4H2O (reduction).
® H2S + 4H2O (reduction).
In the above example, the ratio of the number of electrons participating in the reduction process to that liberated in oxidation is 4:1. To obtain the overall equation of the reaction, we have to take this ratio into account when summing the equations of the reduction and oxidation processes, i.e. multiply the reduction equation by four. It is customary practice to indicate the required multipliers to the right of a vertical line when writing the equations:
2I- = I2 + 2 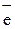 +
SO42- + 10H+ + 8
+
SO42- + 10H+ + 8 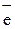 ® H2S + 4H2O ® H2S + 4H2O
| |
| SO42- + 8 I- + 10H+ = 4 I2 + H2S + 4H2O |
The reaction equation obtained can also be written in the molecular form:
H2SO4 + 8HI = 4I2 + H2S + H2O.
Example 2. Reaction of Aluminium with Potassium Nitrate in a basic solution. The skeleton equation is:
KNO3 + Al + KOH + H2O ® NH3 + KAlO2.
Here the oxidation number changes in Nitrogen and Aluminium. Metallic Aluminium (its oxidation number is zero) transforms into the ion A1O2-, in which the oxidation number of the Aluminium is +3. To compile the oxidation equation, we shall proceed from the scheme:
Al ® AlO2-.
In a basic solution, the OH- ion is the source of the Oxygen needed for this process to occur. Four hydroxide ions are required to combine one Aluminium atom into AlO2- ion:
Al + 4 OH- ® AlO2- + 2H2O.
The left-hand side of the formula contains four negative charges, and the right-hand side only one. Hence, in the course of the process, three electrons are given up:
Al + 4 OH- = AlO2- + 2H2O + 3 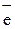 (oxidation).
(oxidation).
To obtain the reduction equation, we shall proceed from the scheme:
NO3- ® NH3.
Here in the course of the process, the Nitrogen atoms lose Oxygen atoms and is combined with Hydrogen atoms. In a basic solution, it is possible with the participation of water molecules. Three water molecules are needed to be combined with three Oxygen atoms, and three more water molecules to form a molecule of NH3:
NO3- + 6H2O ® NH3 + 9 OH-.
The total charge of the right-hand side of the formula is nine negative charges, and of the left-hand side - one. Consequently, eight electrons participate in the process:
NO3- + 6H2O + 8 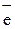 = NH3 + 9 OH- (reduction).
= NH3 + 9 OH- (reduction).
The ratio between the number of electrons liberated in oxidation and the number of electrons gained in reduction is 3:8 in the given example. Hence, to obtain the overall equation of the reaction, we must summate the equations of the oxidation and reduction processes, multiplying the first of them by 8 and the second by 3:
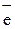
NO3- + 6H2O + 8 | ||||
| 8 Al + 3 NO3- + 5 OH- = 8 AlO2- + 3 NH3 |
or in the molecular form:
8 Al + 3 KNO3 + 5 KOH + 2 H2O = 8 KAlO2 + 3 NH3.
Example 3. Catalytic oxidation of ammonia. This reaction is used in the production of Nitric acid. It is conducted at a temperature of about 7500C. The skeleton equation is:
NH3 + O2 → NO + H2O.
The condensation of water vapor (steam) at 7500C is impossible. We shall therefore not write the equations of the oxidation and reduction processes as we did for reactions proceeding in an aqueous solution - with the participation of water molecules, Hydrogen or hydroxide ions. We shall only count the number of electrons participating in the oxidation and reduction. We shall take into account that the increase in the oxidation number of an element is equal to the number of lost electrons, and the decrease equals the number of gained electrons.
According to the skeleton equation, the oxidation number changes both in the Nitrogen and in the Oxygen. In the former, it grows from - 3 to +2, and in the latter, it diminishes from 0 to -2. Let us write these changes as formulas, indicating the oxidation numbers of the relevant elements as superscripts. To avoid confusion with the charge of an ion, we shall use Roman numerals for this purpose:
N-III → N+II + 5 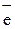 (oxidation);
(oxidation);
O20 + 4 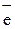 → 2 O-II (reduction).
→ 2 O-II (reduction).
The ratio of the number of electrons gained in reduction to the number of electrons lost in oxidation is 4:5. Hence, five molecules of Oxygen can oxidize four molecules of Ammonia:
4 NH3 + 5 O2 = 4 NO + 6 H2O.
The reaction equations in the above three examples were compiled in a definite sequence. It can also be adhered to in other cases when compiling the equations of redox reactions. The sequence of operations is as follows:
1. Draw up a skeleton equation indicating the reactants and products.
2. Determine the oxidation numbers of the elements in the substances of the right-hand and left-hand sides of the equation; indicate the elements whose oxidation number changes.
3. Draw up the reduction and oxidation equations; find the ratio of the number of electrons gained in reduction to that lost in oxidation.
4. Sum the oxidation and reduction equations with account taken of the ratio of the number of electrons found in point 3.
Date: 2015-01-12; view: 1312
| <== previous page | | | next page ==> |
| Oxidation-Reduction Reactions | | | Most Important Oxidizing and Reducing Agents |