
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Sequentional Circuits
2.1 Circuritry of flips
Transistor T1 is on when a positive voltage is dropped across resistor R1 or resistor R2. If we also take into account the level inversion produced by the transistor, we can see that components R1 , R 2, T1 and RC form a nor gate. The same applies to the other half of the circuit. Inserting the appropriate circuit symbols, we obtain the circuit diagram shown in Fig. 2.1 with the associated truth table (Fig. 2.2).
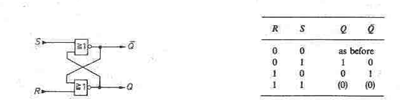 |
Fig. 2.1 - Flip-flop comprising nor gates. Fig. 2.2 - Truth table.
Sequential logic systems
A sequential logic system is an arrangement of digital circuits which can carry out logic operations and, in addition, store the states of individual variables. It diners from a combinatorial logic system in that the output variables yj are not only dependent on the input variable xi, but also on the previous history which is represented by the state of flip-flops.
In the following we shall first discuss the design and operation of integrated flip-flops.
Integrated flip-flops
We shall now demonstrate the operation of flip-flops with reference to gates. This approach defines their basic operation irrespective of the particular technology employed.
Transparent flip-flops
By connecting two NOR gates in a feedback arrangement as in Fig. 2.3, we obtain a flip-flop which has complementary outputs Q and 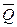 and two inputs S (Set) and R (Reset).
and two inputs S (Set) and R (Reset).
If the complementary input state S = 1 and R = 0 is applied, we have
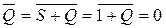
and
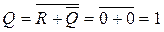
The two outputs, therefore, assume complementary states. Similarly, for R = 1 and S = 0, the opposite output state is obtained. If we make R = S = 0, the old output state is retained. This explains why RS flip-flops are used as memories. When R = S = 1, the two outputs become simultaneously 0; however, the output state is no longer defined when R and S then become simultaneously 0. Consequently, the input state R = S = 1 is generally disallowed. The switching states are summarized in the truth table in Fig. 2.4, with which we are already familiar from the transistor circuit
In Section 9.2 we showed that a logic equation does not change if all the variables are negated and the arithmetic operations (+) and (•) are interchanged. Applying this rule here, we arrive at the RS flip-flop comprising NAND gates shown in Fig. 2.5, which has the same truth table as that shown in Fig. 2.4. However, note that the input variables are now  and
and 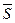 . As we shall be frequently using the RS flip-flop comprising NAND gates, we have given its truth table for input variables
. As we shall be frequently using the RS flip-flop comprising NAND gates, we have given its truth table for input variables  and
and 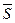 in Fig. 2.6.
in Fig. 2.6.

Fig. 2.3 - RS flip-flop comprising NOR gates. . Fig. 2.4 - Truth table for an RS flip-flop.

Fig. 2.5 - RS flip-flop comprising NAND gates Fig. 2.6 .- Truth table for an RS flip- flop comprising NAND gates.
Date: 2015-01-12; view: 1515
| <== previous page | | | next page ==> |
| Window comparator | | | Clocked RS flip-flop |