
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Binary Decoders
An n-input binary decoder (Figure1.19) is a combinational system that has n binary inputs x = (xn-1 , . . . , x0) and 2n binary outputs y = ( 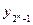 , . . . , y0). The input vector x can be considered as representing integers from 0 to 2n-1 in the radix-2 representation. When the input represents the integer i, then yi, is equal to 1 and all other outputs are equal to 0. To facilitate the use of decoder modules in designing networks, an additional input, called module enable E, is provided. When E=0, all module outputs are 0 (or three-state).
, . . . , y0). The input vector x can be considered as representing integers from 0 to 2n-1 in the radix-2 representation. When the input represents the integer i, then yi, is equal to 1 and all other outputs are equal to 0. To facilitate the use of decoder modules in designing networks, an additional input, called module enable E, is provided. When E=0, all module outputs are 0 (or three-state).
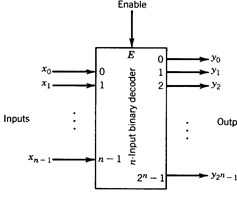
Fig. 1.19 - n-Input binary decoder.
A high-level description of an n-input binary decoder is
| yi= | 1 if x=i and E=1 |
| 0 otherwise |
where
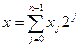
and
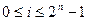
In the description of systems that use this module, the decoder function is denoted by
y=DEC(x,E)
For example, DEC((l,l,0),l) = (0,1,0,0,0,0,0,0).
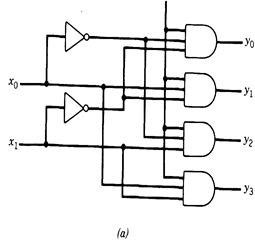
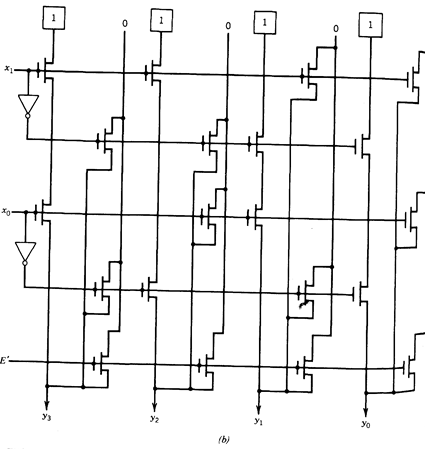
Fig. 1.20 - Implementation of 2-input binary decoder,(a) with getes and (b) with pass transistor.
The switching expressions that represent a binary decoder are
yi=Emi(x)
where, as defined in Chapter 3, mi(x) is the ith minterm of the n variables x.
An implementation of a 2-input binary decoder using gates is illustrated in Fig.1.20.a and a pass-transistor implementation is shown in Figure 1.20.b. A binary decoder is used whenever a set of values has been encoded using a binary code and they have to be separated, that is, decoded. As an example, consider operation code in a computer. This code is part of every instruction and allies the operation to be executed.
Decoders exist for other representations of the input integer. For example, decimal decoders having ten outputs exist for codes such as BCD and Excess-3. Their definition and implementation are similar to those of the binary decoder.
An Excess-3 decoder has four inputs representing a decimal digit in the Excess-3 code and ten outputs. The ith output is 1 when the input represents the integer i. The Excess-3 code is given in the following table:
| i | X3 | X2 | X1 | X0 |
A high-level description of the Excess-3 decoder
| Y= | 1 if x=i and 0 £ i £ 9 |
| 0 otherwise |
where
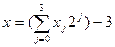
The switching expression for the ith output is
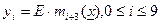
The design of n-input binary decoders using k-input binary decoders, k < n and the use of the binary decoder as a universal module are discussed in the following sections.
Date: 2015-01-12; view: 2163
| <== previous page | | | next page ==> |
| Decoder | | | Decoder Networks |