SOME METHODS OF DETERMINATION OF DISTANCE IN ASTRONOMY

I. Parallax method. It seems to us that stars are located at identical distance from us, as well as distant mountains on the horizon. It is established that light traveling at the great speed (300 thousand km/s) from the nearest star reaches the Earth in 4.3 years. At such huge distances we can't notice with the unaided eye neither movements of stars relatively each other, nor their sizes and also to determine distance to them. Nevertheless the distance to the celestial bodies closest to the Earth (especially bodies of Solar system and the nearest stars) can be determined by applying the method based on simultaneous observation of bodies from two widely separated points. This method in astronomy is called a parallax method.

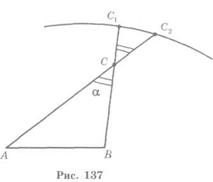
Parallactic shift is the difference in the apparent position of an object viewed along two different lines of sight. For measurement of the magnitude of a parallactic shift we will observe the object C from points A and B. Projections of this object on the celestial sphere we will denote by points C₁ and C₂. Parallactic shift of the object C viewed along two different lines of sight is measured by angle a (fig. 137).

The segment AB is called the baseline and the angle a subtended by the baseline at a point C is called the parallax. The Earth radius is taken as the baseline to determine the distances to objects of the Solar system.

Really, in the course of daily rotation of the Earth the observer on its surface appears on opposite positions relative to the Earth¢s center. Therefore the objects of the Solar system appear to move against the background stars on the celestial sphere. The situation is demonstrated in the fig. 138. The angle р at which the Earth radius is seen to be perpendicular to the observer from the star is called the horizontal parallax. From the triangle COB the distance to bodies of the Solar system can be found by the formula

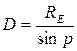
where R_E = 6378 km is the Earth radius.

As the Moon is the closest celestial body to the Earth its parallax is of the greatest value p_M = 57'.

Due to the parallax there are the following circumstances related with the rising and setting of the Moon. The observer, who is on the equator at the point A (fig. 138), will see the rising Moon among stars almost on 2° displaced «to the left», than the other observer who sees at the same time at the point B the set of the Moon. Also due to the parallax the Moon rises nearly for 2 minutes later and sets the same minutes earlier, than it is specified in astronomical year-books.

Fig. 138

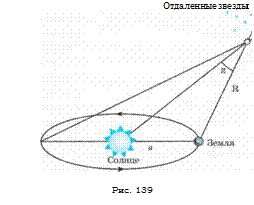To determine the distances to the nearby stars it is necessary to observe them from two opposite points of the Earth¢orbit around the Sun. For this purpose the radius of the Earth¢orbit is taken as the baseline.

The angle p at which the radius of the Earth¢orbit is seen to be perpendicular to the observer from the star is called the annual parallax p (fig. 139). So the distance R to the star equals:

.

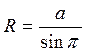The annual parallax of all stars is very small - it is always less than 1". The star having an annual parallax of 1" is at the following distance from the Earth: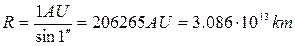

The distance to the star that has the annual parallax of 1" makes one parsec (from the words «parallax» and «second»). The distances to the stars measured in parsecs (pc) are calculated by a very simple formula: 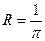(pc). The star closest to Earth is the Proxima Centauri. Its annual parallax is equal to 0.76". Hence, the distance to the star is .

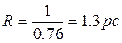II. The radio-echo method is based on sending a powerful short radio-frequency pulse towards a celestial body and receiving the signal reflected from it. The speed of radio wave propagation is equal to the speed of light in vacuum c = 299792 458 m/s. Therefore the accurate measurement of the time taken for the signal in going to the celestial body and coming back to the Earth makes it easy to calculate the distance to the celestial body. The radio-echo method allowed to measure with a big accuracy the distances from the Earth to many bodies of the Solar system: Moon, Venus, Mercury, Mars, Saturn and Jupiter.

Determination of the value of the astronomical unit with a big accuracy is of great significance for space flights. Just a few years ago the accuracy of measurement of astronomical units was low: the error was more than 0,5% that equaled to tens of thousands kilometers. The radio-echo observations of the Venus allowed determining the astronomical unit with a big accuracy:

1AU = 149 597 868 ± 0.7 km

The rounded value of the astronomical unit (149 600 000 km) corresponds to solar parallax of р = 8.7940".

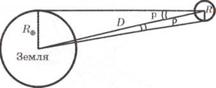
III. Determination of the sizes of Solar system bodies. The angular sizes of the Solar system bodies, i.e. the angles subtended at the observer on the Earth surface by the diameters of the celestial bodies, are determined using special methods. If the angular radius r of the celestial body is known and its distance from the Earth is equal to D then it is possible to calculate its linear radius R (fig. 140): R = D×sinr. The distance to the body is 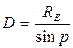, so we find:

.

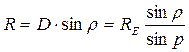As the angles r and p are of small value then:

.

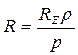Example. It is known that the angular radius of the Sun is r = 16'. The horizontal parallax of the Sun is р = 8.8". By how much is its linear radius greater than the linear radius of the Earth?

Information given:

r = 16'

р = 8.8"

--------------------

R_S = ?

Solution: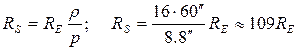

Self-testing questions

1. What is the essence of the phenomenon of parallactic shift?

2. What is the parallactic shift?

3. How is the distance to a remote point measured by the parallax method?

4. What is the horizontal parallax of a star?

5. What is the annual parallax of a star?

6. How is the distance to a star determined by an annual parallax?

7. How is the diameter of the planet determined if the distance to the planet and the angle subtended at the observer by its radius are known?

Exercise 36

1. Having known the radius of the Earth (R_E = 6378 km) and the horizontal parallax of the Moon (p = 57'), calculate the radius of the Moon.

2. Assuming that the angular sizes of the Sun and the Moon are equal and having known their horizontal parallaxes (8.8" and 57' respectively), calculate by how much is the Sun radius greater than the Moon radius?

3. What is the linear diameter of the Saturn¢s ring if from the distance of 1.3×10⁹ km it is visible at an angle of 40^o?

4. The angular diameter of the Sun is 32¢ and its linear diameter by¢ 109 times greater than that of the Earth. From what distance would the planet with a diameter equal to the terrestrial and angular size equal to the solar be visible?

5. When the Mars is at its nearest distance to the Earth (r =5.6 ×10⁷км) its angular diameter is 25¢¢. What is its linear diameter?

6. Parallax of a star is 0.5¢¢. Determine by how much is this star farther from us than the Sun?

7. Parallax of the Altair is 0.12¢¢. Determine the distance to this star in: parsecs, light years; astronomical units; kilometers.

Date: 2015-01-12; view: 511