LAWS OF MOVEMENT OF PLANETS OF SOLAR SYSTEM

The Polish scientist Nicolaus Copernicus (1473-1543) in his heliocentric model of the Solar system used the idea of the ancients that planets move along circular orbits with constant speed.

Only at the beginning of the XVII century it was established that orbits of celestial bodies actually differ from a circle. This discovery was made by the German astronomer Johannes Kepler (1571-1630).

Kepler found that the positions of planets calculated according to the model of Copernicus differ from the positions determined by observations. Therefore, it was necessary to refuse the assumption that planets move round the Sun along a circle. To determine trajectories and laws of planets¢s motion he used the results of very accurate observations of Mars obtained by the Danish astronomer Tycho Brahe (1546 - 1601). Years of his work resulted in 1609-1619 by discovery of three laws of planetary motion called Kepler's law, in his honor.

I. Kepler's first law determines the shape of a planet¢s orbit: the orbit of each planet is an ellipse, with the Sun at one focus of the ellipse.

The ellipse has the symmetry center at point O, two axes of symmetry AA₁ = 2а and BB₁ = 2b, where a is the semimajor axis and b is the semiminor axis (fig. 135). Its two focuses are located at the distance OF₁ = OF₂ = c = a² - b² from the center.

The main property of the ellipse is the following: the sum of distances to the foci from any point M on the ellipse is a constant equal to the double length of the semimajor axis:

MF₁ + MF₂ = 2а.

Eccentricity of the ellipse is the ratio of the focus distance from the ellipse center to its semimajor axis:

e = c:a.

The greater is е the more is the amount of flattening of the ellipse. If c = 0 (the foci coincide with the center) then е = 0, so the ellipse transforms into a circle with radius a.

The orbits of Venus and Earth are nearly circular in shape (eccentricity of Venus¢s orbit is е = 0.0068 and of Earth¢s is e = 0.0167). The orbits of other planets are more eccentric. The point of an orbit nearest to the Sun is called the perihelion (from the Greek words peri - «near» and helios - «the Sun»), and the most remote point is called aphelion (from the Greek word aphelios meaning apho-«remote» and helios - «the Sun»). The semimajor axis of the ellipse equals the average distance of the planet from the Sun. In astronomy the average distance between the Earth and the Sun, i.e. the average radius of the Earth ¢s orbit, is taken as the unit of measurement for distances in the solar system, which is termed an astronomical unit (AU):

1 AU » 149 600 000 km

The shortest distance from the Earth to the Moon or to the artificial satellite of the Earth is called perigee (from the Greek Gaea - «the Earth») and the farthest distance is called apogee.

II. Kepler's second law (the law of the areas) determines that planet moves along its orbit round the Sun nonuniformly:

a line joining a planet and the Sun sweeps out equal areas during equal intervals of time.

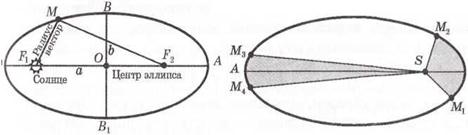
Fig.135 Fig.136

Let the sectors SM₁M₂ and SM₃M₄ be of equal areas as it is shown in fig.136. The distances covered by the planet during equal intervals of time, are various. Apparently the shorter is the line joining the planet and the Sun the greater is the length of an arch, therefore, the more is the orbital speed of the planet. The planet moves with maximum speed when it is near perihelion and with minimum speed when it is near aphelion.

III. Kepler's third law determines the relationship between the orbital period of a planet and its average distance from the Sun:

the ratio of the squares of the sidereal periods for two planets revolving round the Sun is equal to the ratio of the cubes of their semimajor axes.

Let the semimajor axes for two planets be denoted by a₁ and a₂, the periods of their revolution by T₁ and T₂. Then

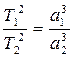
Newton, after discovering the law of universal gravitation, generalized Kepler's third law. He proved that if two bodies with masses M₁ and M₂ revolving round the common center of gravity with the period T at the distance a from each other then the following ratio is valid:

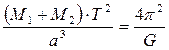
On the basis of this ratio it is possible to calculate the masses of the celestial bodies. For an example, let us to determine the mass of the Sun in terms of the mass of Earth by the known values of the periods and distances for the systems Earth- Sun and Earth -Moon. Let us write down the previous ratio for the system Earth- Sun:

where M_S is the mass of the Sun; M_E is the mass of the Earth; T_E is the period of the Earth revolution; a_E is the semimajor axes of the Earth¢s orbit. For the system Earth-Moon:

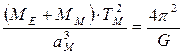
where M_M is the mass of the Moon; T_M is the period of the Moon revolution; a_M is the semimajor axes of the Moon¢s orbit.

Equating the left parts of expressions and neglecting the mass of the satellite in comparison with the mass of the central body, we find the mass of the Sun, expressed in terms of the mass of the Earth:

In the same way the mass of any planet is determined by comparing the data on the systems Earth-Moon and planet-satellite.

Further it was proved that Kepler's laws are applicable not only to the Solar system, but also to any system of celestial bodies.

Example. The semimajor axes of the Mars¢s orbit is 1,5 AU. Calculate the period of its revolution round the Sun.

Information given:

a₁ = 1.5 AU

a₂ = 1 AU

T₂ = 1 year

-----------------------

T₁ = ?

Solution: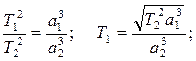

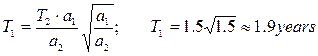
Self-testing questions

1. What is the statement of the Kepler¢s first law?

2. What does the Kepler¢s second law state?

3. At what points the speed of planet¢s motion along an orbit is maximum and minimum?

4. How does the value of planet¢s speed change during its motion from the aphelion to the perihelion?

Exercise 35

1. Uranium period of revolution round the Sun is 84 years. How much time the distance of the Uranium from the Sun is further than distance of the Earth from the Sun?

2. The semimajor axes of the Jupiter¢s orbit is 5 AU. What is the period of its revolution round the Sun?

Date: 2015-01-12; view: 2358