Equations and Identities

An equation is a statement of equality between two algebraic expressions. The two expressions are called members, or sides of the equation. If the two members of an equation are finite and are exactly the same, or become the same, for every value of the symbols or variables involved, the equation is called an identical equation or an identity, for example

(x - 2)² = x² - 4х + 4, (x + 3) (x - 2) = x² + x - 6

If the two members of an equation are equal for certain particular values of the symbols involved, but not for all values, the equation is called a conditional equation, or briefly, an equation. An equation in one unknown, say x, is a way of describing one or more numbers by stating a condition the numbers must satisfy. To solve an equation is to find values of the unknowns that make the two members equal. Such values of the unknowns are called roots or solutions of the equation.

The following rules aid in finding the root.

1. The roots of an equation remain unchanged if the same expression is added to or subtracted from both sides of the equation.

2. The roots of an equation remain the same if both sides of the equation are multiplied or divided by the same expression other than zero and not involving the letter whose value is in question.

The equation 2x = 4, where x is the unknown, is true for x = 2. To illustrate the first of the above two rules, add 5x to both sides of the equation 2x = 4. We get 2x + 5x = 4+5x which, like equation 2x = 4, is true for only x = 2. To illustrate the importance of the restriction in the second of the above two laws, multiply both sides of the equation by x and get

(2x) x = (4x) x which is true not only for x = 2, but also for x = 0.

It is always a good plan to check the accuracy of one's work by substituting the result in the original equation to see whether the equation is true for this value.

These numbers or values of the unknown x actually satisfy the equation upon substitution.

For convenience equations are classified in various ways; according to degree they may be linear, quadratic, cubic, etc.; in form, integral or fractional, rational or irrational. Regardless of the form the equation is in at first, the process of solving will involve transformations which will finally put it in the form:

the unknown = one or more definite values

Those transformations when applied to an equation will give a new or derived equation. A derived equation is said to be equivalent with respect to an original equation if it contains all the roots of that equation and no others. The following operations will always lead to equivalent equations, i.e.

1. Adding to or subtracting the same finite quantity from both members.

2. Multiplying or dividing both members by the same quantity provided this quantity is not zero and does not contain the unknown.

If the equation is fractional it may be changed into an integral equation by multiplying both sides by the Least Common Denominator. This process is called clearing the equation of fractions. The integral equation will have all the roots of the original fractional equation but sometimes will include additional roots. These extraneous roots will be values of the unknown for which the Least Common Denominator is zero and they can readily be recognized and discarded.

An equation in which the variable is raised to the first power only is usually called a linear, or first degree, equation.

To solve an equation containing fractions, first reduce each fraction to its lowest terms. Then multiply each side of the equation by the Least Common Denominator of all the denominators. This process is called clearing of fractions.

A quadratic equation is one which can be reduced to the form

2ax + bx + с = 0 (a 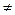0) where a, b and с are known and x is unknown.

Date: 2015-01-11; view: 1015