Rational numbers and decimal numerals

In mathematics, a fraction is a concept of a proportional relation between a part and a whole. In other words, it is an example of a specific type of ratio, in which the two numbers are related in a part-to-whole relationship, rather than a comparative relation between two separate quantities.

A fraction is a quotient of numbers, the quantity obtained when the numerator is divided by the denominator. Thus, ¾ represents three divided by four.

The denominator represents the number of equal parts that an object is divided into, and the numerator tells the number of those parts indicated for the particular fraction. The numeratorand the denominator of a fraction may be separated by a slanting line (e.g. ½), or may be written above and below a horizontal line.

Fractions are rational numbers and that means that the denominator and the numerator are integers. Any rational number might be defined as a number named by 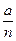where a and n ≠ 0.

Usually there are several ways of reading fractions. One may say ‘three quarters’ for 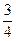and ‘one sixth’ for 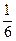. In strictly mathematical contexts these fractions might also be read as ‘three over four’, ‘one over six’ or ‘three upon four’, ‘one upon six’. Especially more complex fractions may be expressed by using the word ‘over’ (e.g. ).

A common fraction is called a proper fraction if the absolute value of the numerator is less than the absolute value of the denominator – that is, if the absolute value of the entire fraction is less than one. An improper fraction names the absolute value of the numerator greater than or equal to the absolute value of the denominator (e.g. 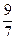, 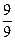). A mixed number is the sum of a whole number and a proper fraction. This sum is implied without the use of ‘+’ sign (e.g. 1 ).

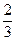Fractions which represent the same fractional number like , , 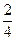, 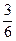and so on, are called equivalent fractions.

You have already known that any fractional number multiplied by one has the same value as the original number (e.g. 1 = ).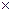

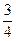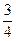As soon as we have multiplied the numerator and the denominator of a fraction by the same (non-zero) number, the resulting fraction will be equivalent to the original fraction. We simply produce another name for the fraction. Consider the fraction . When both the numerator and the denominator are both multiplied by two, the result is 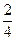which has the same value as .

Dividing the numerator and the denominator by the same non-zero number we just reduce or simplify the fraction. A fraction in which the numerator and the denominator have no factors in common other than 1 is called irreducible or in its lowest or simplest terms. Consider the following fractions: 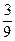and 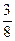. The former is not in the lowest terms because both 3 and 9 can be divided by 3. In contrast 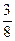is in lowest terms – the only number that is a factor of both 3 and 8 is 1.

A decimal fraction is a special type of fraction written without a denominator (which is 10 or a power of 10) but in which the number of figures on the right-hand side of a dot, called the decimal point, indicates whether the denominator is 10 or a higher power of 10. All digits to the left of the decimal point represent whole numbers, and all digits to the right of the decimal point represent fractional parts of one.

Decimals like .111, .3535, .282828 are called repeating decimals and those, which repeat zeros, - terminating decimals (e.g. 0.25000).

We have just studied different types of decimals. It’s important to know how decimals are read nowadays. Let’s take such numerals as 9.3 (nine point three), 21.65 (twenty-one point six five), 0.182 (nought point one eight two or zero point one eight two).

Rational numerals can be named by decimal numerals. The arithmetic of numbers in decimal form is in full agreement with the arithmetic of numbers in fractional form.

Date: 2015-01-11; view: 1852