Brief theoretical information

When connecting a capacitor C to a source of constant EMF E resistor with resistance R transition process, as follows from the second Kirchhoff law, described by the equation

R ∙ C ∙ + = E,

where u_? is the instantaneous voltage on the capacitance.

The solution to this equation is an expression

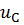= E ∙ (1 ̶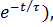

where τ = R ∙ C is the time constant of the circuit.

If the capacitor at the time of connection to the source of constant EMF was charged to a voltage U_C0, the voltage on it will change according to the law

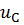= E ̶ (? ̶ ) ∙

The charge current of the capacitor

i = (E ̶ u_C) / R.

The transition process at the discharge of the capacitor to the resistor according to the second Kirchhoff law is described by the equation

R ∙ C ∙ + = 0.

The solution to this equation is an expression

= ∙

The discharge current of the capacitor

i = u_C/ R.

When connecting an ideal coil with inductanceL to a source of constant EMF E through a resistor with resistance R, the transition process in accordance with the second Kirchhoff's law is described by the equation

L ∙ 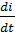+ ∙ R = E,

where i_L instantaneous current through the coil.

The solution of this equation is written in the form of

= (1 ̶

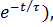
where τ = R / L is the time constant of the circuit.

If the current I_L0 flows through the ideal inductor at the moment of its connection to the source of a constant EMF, then the transition process according to the second Kirchhoff's law is described by the following expression

i_L = E / R ? (E / R ? I_L0) ∙ .

The voltage on the inductor when connected to its EMF source;

u_L = E ? i_L∙ R.

The transition process when switching off the ideal inductor from the EMF source, if the current IL0 flowed through IT before switching off, and its conclusions remain attached to the resistor with resistor Rsh, is described by the equation

L ∙ 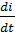+ ∙ R_sh = 0.

This equation has the following solution

= I_L0∙

The voltage on the inductor in this case

u_L = i_L∙ R.

Date: 2018-08-27; view: 26937