Brief information from the theory

The three-phase system was first created to solve the problem of converting electrical energy into mechanical energy by creating a circular rotating magnetic field. It is widespread due to the simplicity of the three-phase asynchronous motor.

The main elements of three-phase circuits are three-phase generator, three-phase transformer, single-phase or three-phase load and connecting wires.

A three-phase generating system can be created from three single-phase sources, the EMF of which can be represented by expressions:

e_A = E_Am ∙ sin ω ∙ t;

e_B = E_Bm ∙ sin (ω ∙ t + 240⁰);

e_C = E_Cm ∙ sin (ω ∙ t + 120⁰).

In complex form these EDS can be recorded:

E_A = E_Am ∙ e ^{j∙ω t};

E_B = E_Bm ∙ e^{(ϳ∙ω∙t-120˚)} ;

E_C = E_Cm ∙ e^{(ϳ∙ω∙t-240 ˚)}.

The time diagram of the three-phase voltage generator is shown in fig. 5.1.

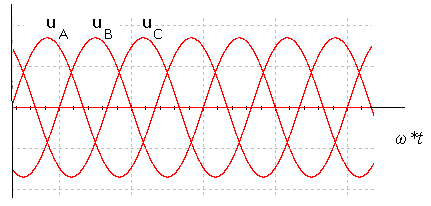
Fig. 5.1. The timing diagram of voltages of three-phase generator

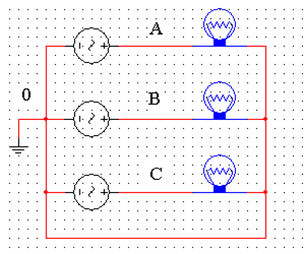
Most often, the energy systems of industrial, administrative and residential complexes will be implemented according to the star-star scheme with a zero wire, as shown in fig. 5. 2 a, sometimes under the scheme "star" - "star" shown in fig. 5..2 b.

There are the following types of three-phase loads.

1. A symmetrical load, which is equal to the complex impedance voltages phase of the receiver:

Z_A = Z_B = Z_C = Z_A ∙ .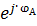

a

b

Fig. 5. 2. Connection scheme of three-phase systems: a ? ?star? - ?star? with zero wire, b ? ?star? - ?star?

1. Uniform load at which the resistance modules of the receiver phases are equal:

Z_A = Z_B = Z_C.

2. Uniform load, which is equal to the arguments of the resistance and the phase of the receiver:

ⱷ_A = ⱷ_B = ⱷ_C.

3, Asymmetric load at which resistance complexes are not equal in all phases of the receiver:

Z_A ≠ Z_B ≠ Z_C.

For the ?star? - ?star? scheme with zero wire under arbitrary load, the following relations are valid for the phase current complexes

I_a = U_a / Z_a ; I_b = U_b / Z_b ; I_c = U_c / Z_c.

For neutral current (zero wire):

I₀ = I_a + I_b + I_c .

For linear and phase voltages of the same circuit

U_l = ∙ U_ph.

At symmetric load, the phase current modules are equal to each other

I_a = I_b = I_c = U_ph / Z_ph,

and the current in the neutral is zero

I₀ = 0.

For the "star" - "star" schema without neutral for arbitrary load neutral voltage

U_N = (U_A * Y_a+ U_B ∙ Y_b + U_C∙ Y_C) / (Y₀ + Y_a + Y_b + Y_c).

The voltage on the load phases,,

U?_a = U_A̶ U_N ; U?_b = U_B̶ U_N ; U?_c = U_C̶ U_N.

The currents in the phases of the load:

I_a = U?_a / Z_? ; I_b= U?_b/ Z_b ; I_c= U?_c/ Z_c..

At the same time, in each phase of the circuit, a complex linear currents is equal to the phases current.

I_l = I_ph .

Phase shift angles between phase currents and voltages

ⱷ_a = arctg (X_a / R_a); ⱷ_b = arctg (X_b / R_b); ⱷ_c = arctg (X_c / R_c),

where R_a, R_b, R_c ? resistance of the load phases;

X_a, X_b, X_c ? their reaction resistances.

Active power of three-phase circuit under arbitrary load

P = P_a + P_b + P_c ;

reactive power

Q = Q_a + Q_b + Q_c ;

full power

S = .

With a symmetrical load

P = 3 ∙ U_ph ∙ I_ph ∙ cos ⱷ_l = ∙ U_l ∙ I_l ∙ cos ⱷ_l;

Q = 3 ∙ U_ph ∙ I_ph ∙ sin ⱷ_l = ∙ U_l ∙ I_l ∙ sin ⱷ_l;

S = 3 ∙ U_ph ∙ I_ph = ∙ U_l ∙ I_l .

Date: 2018-08-27; view: 28021