
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Hölder bərabərsizliyi

Bir çox hallarda qısa olaraq  metrik fəzasının əvəzinə X kimi də yazırlar. Daha doğrusu, X metrik fəzası verilmişdir dedikdə X çoxluğu və bu çoxluqda verilmiş metrika başa düşülür. Tutaq ki,
metrik fəzasının əvəzinə X kimi də yazırlar. Daha doğrusu, X metrik fəzası verilmişdir dedikdə X çoxluğu və bu çoxluqda verilmiş metrika başa düşülür. Tutaq ki,  metrik fəzası verilmişdir. Aydındır ki, X çoxluğunun
metrik fəzası verilmişdir. Aydındır ki, X çoxluğunun  altçoxluğunda da metrikanı
altçoxluğunda da metrikanı  kimi daxil etmək olar. Onda
kimi daxil etmək olar. Onda  metrik fəzasına
metrik fəzasına  metrik fəzasının altfəzası deyilir.
metrik fəzasının altfəzası deyilir.
Tutaq ki,  metrik fəzaları və
metrik fəzaları və 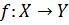 inikası verilmişdir.
inikası verilmişdir.
Tərif:Tutaq ki,  ədədinə görə
ədədinə görə  var ki,
var ki,  şərtini ödəyən
şərtini ödəyən  elementi üçün
elementi üçün  şərti ödənilir. Onda f inikası
şərti ödənilir. Onda f inikası  nöqtəsində kəsilməz adlanır.
nöqtəsində kəsilməz adlanır.
Tutaq ki,  metrik fəzaları və
metrik fəzaları və 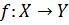 inikası verilmişdir. Əgər f inikası qarşılıqlı birqiymətli və f ,
inikası verilmişdir. Əgər f inikası qarşılıqlı birqiymətli və f , 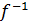 inikasları X çoxluğunda kəsilməz olarsa, f inikası homoemorf inikas, X və Y metrik fəzaları isə homoemorf fəzalar adlanır.
inikasları X çoxluğunda kəsilməz olarsa, f inikası homoemorf inikas, X və Y metrik fəzaları isə homoemorf fəzalar adlanır.
Tutaq ki,  metrik fəzaları verilmişdir və və
metrik fəzaları verilmişdir və və 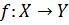 inikası biyektivdir. Əgər
inikası biyektivdir. Əgər 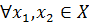 üçün
üçün  olarsa,
olarsa,  metrik fəzaları izometrik metrik fəzalar adlanır.
metrik fəzaları izometrik metrik fəzalar adlanır.
MÜHAZİRƏ 3.METRİK FƏZADA ƏTRAF ANLAYIŞI
Tutaq ki,  metrik fəzası,
metrik fəzası,  nöqtəsi və
nöqtəsi və  ədədi verilmişdir.
ədədi verilmişdir.
 şərtini ödəyən bütün mümkün
şərtini ödəyən bütün mümkün  nöqtələr çoxluğunun əmələ gətirdiyi çoxluq mərkəzi
nöqtələr çoxluğunun əmələ gətirdiyi çoxluq mərkəzi  nöqtəsi olan r radiuslu qapalı kürəadlanır.
nöqtəsi olan r radiuslu qapalı kürəadlanır.
 şərtini ödəyən bütün mümkün
şərtini ödəyən bütün mümkün  nöqtələr çoxluğuna mərkəzi
nöqtələr çoxluğuna mərkəzi  nöqtəsi olan r radiuslu açıq kürədeyilir.
nöqtəsi olan r radiuslu açıq kürədeyilir.
Mərkəzi  nöqtəsi olan
nöqtəsi olan  radiuslu açıq kürəyə
radiuslu açıq kürəyə  nöqtəsinin
nöqtəsinin  ətrafı deyilir və
ətrafı deyilir və  kimi işarə olunur.
kimi işarə olunur.
 çoxluğuna
çoxluğuna  nöqtəsinin
nöqtəsinin  deşilmiş ətrafı deyilir.
deşilmiş ətrafı deyilir.
Tərif 1: Tutaq ki,  çoxluğu verilmişdir. Əgər
çoxluğu verilmişdir. Əgər  nöqtəsinin
nöqtəsinin  ətrafı ilə M çoxluğunun kəsişməsi boş deyilsə,
ətrafı ilə M çoxluğunun kəsişməsi boş deyilsə,  nöqtəsi M çoxluğunun toxunma nöqtəsiadlanır.
nöqtəsi M çoxluğunun toxunma nöqtəsiadlanır.
Tərif 2: M çoxluğunun bütün toxunma nöqtələri çoxluğuna M çoxluğunun qapanmasıdeyilir və  kimi işarə olunur.
kimi işarə olunur.
Qeyd edək ki, çoxluğun qapanması əməliyyatı aşağıdakı xassələri ödəyir:
1) 
2) 
3) 
4) 
Tərif 3: Əgər  olarsa, M çoxluğuna qapalı çoxluqdeyilir.
olarsa, M çoxluğuna qapalı çoxluqdeyilir.
Tərif 4:Əgər  nöqtəsinin
nöqtəsinin  deşilmiş ətrafı ilə M çoxluğunun kəsişməsi boş deyilsə,
deşilmiş ətrafı ilə M çoxluğunun kəsişməsi boş deyilsə,  nöqtəsi M çoxluğunun limit nöqtəsiadlanır.
nöqtəsi M çoxluğunun limit nöqtəsiadlanır.
Tərif 5: Tutaq ki,  və
və  nöqtəsinin
nöqtəsinin  deşilmiş ətrafı var ki, bu ətraf ilə M çoxluğunun kəsişməsi boş çoxluqdur. Onda
deşilmiş ətrafı var ki, bu ətraf ilə M çoxluğunun kəsişməsi boş çoxluqdur. Onda  nöqtəsi M çoxluğunun izoləedilmiş nöqtəsiadlanır.
nöqtəsi M çoxluğunun izoləedilmiş nöqtəsiadlanır.
Təriflərdən aydındır ki,çoxluğun toxunma nöqtəsi ya çoxluğun limit nöqtəsidir ya da izoləedilmiş nöqtəsidir.
MÜHAZİRƏ 4.METRİK FƏZADA YIĞILMA
Tutaq ki,  metrik fəzası və
metrik fəzası və  ardıcıllığı verilmişdir. Əgər
ardıcıllığı verilmişdir. Əgər

olarsa,  nöqtəsinə
nöqtəsinə  ardıcıllığının limitideyilir. Metrik fəzada ardıcıllığın limitinə aşağıdakı kimi də tərif vermək olar.
ardıcıllığının limitideyilir. Metrik fəzada ardıcıllığın limitinə aşağıdakı kimi də tərif vermək olar.
Tərif 1: Tutaq ki,  ədədinə görə
ədədinə görə  nömrəsi var ki,
nömrəsi var ki,  üçün
üçün 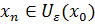 şərti ödənilir. Onda
şərti ödənilir. Onda  nöqtəsinə
nöqtəsinə  ardıcıllığının limitideyilir və
ardıcıllığının limitideyilir və

kimi işarə olunur.
Teorem 1: Tutaq ki,  metrik fəzası və
metrik fəzası və  çoxluğu və
çoxluğu və  nöqtəsi verilmişdir.
nöqtəsi verilmişdir.  nöqtəsinin M çoxluğunun limit nöqtəsi olması üçün zəruri və kafi şərt
nöqtəsinin M çoxluğunun limit nöqtəsi olması üçün zəruri və kafi şərt  ardıcıllığının olmasıdır ki,
ardıcıllığının olmasıdır ki,

olsun.
İsbatı:(zərurilik)Tutaq ki,  nöqtəsi M çoxluğunun limit nöqtəsidir. Onda limit nöqtəsinin tərifinə əsasən
nöqtəsi M çoxluğunun limit nöqtəsidir. Onda limit nöqtəsinin tərifinə əsasən 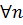 natural ədədi üçün
natural ədədi üçün 
Onda 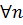 natural ədədi üçün
natural ədədi üçün  nöqtəsi götürək. Onda aydındır ki, bu qaydayla qurulan ardıcıllıq üçün
nöqtəsi götürək. Onda aydındır ki, bu qaydayla qurulan ardıcıllıq üçün  olar. Axırıncı daxil olmadan aydındır ki,
olar. Axırıncı daxil olmadan aydındır ki,

(kafilik):

olduğundan tərifə əsasən  ədədinə görə
ədədinə görə  nömrəsi var ki,
nömrəsi var ki,  üçün
üçün 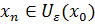 olar. Digər tərəfdən
olar. Digər tərəfdən  olduğundan alarıq ki,
olduğundan alarıq ki,  nöqtəsi M çoxluğunun limit nöqtəsidir. Teorem isbat olundu.
nöqtəsi M çoxluğunun limit nöqtəsidir. Teorem isbat olundu.
MÜHAZİRƏ 5.TAM METRİK FƏZA
Tutaq ki,  metrik fəzası və
metrik fəzası və  ardıcıllığı verilmişdir.
ardıcıllığı verilmişdir.
Tərif 1: Tutaq ki,  ədədinə görə
ədədinə görə  nömrəsi var ki,
nömrəsi var ki,  ,
,  üçün
üçün  şərti ödənilir. Onda
şərti ödənilir. Onda  ardıcıllığına fundamental ardıcıllıq deyilir.
ardıcıllığına fundamental ardıcıllıq deyilir.
Teorem 1: Hər bir yığılan ardıcıllıq fundamentaldır.
Isbatı : Tutaq ki,

Onda limitin tərifinə əsasən  ədədinə görə
ədədinə görə  nömrəsi var ki,
nömrəsi var ki,  üçün
üçün  olar. Onda metrikanın 3-cü xassəsinə əsasən(üçbucaq aksiomu)
olar. Onda metrikanın 3-cü xassəsinə əsasən(üçbucaq aksiomu)  ,
,  üçün
üçün  olar. Bu isə o deməkdir ki,
olar. Bu isə o deməkdir ki,  ardıcıllığı fundamentaldır. Teorem isbat olundu.
ardıcıllığı fundamentaldır. Teorem isbat olundu.
Ümumuiyyətlə desək, bir çox fəzalarda fundamental ardıcıllıq yığılan olmaya da bilər.
Tərif 2: Tutaq ki, (  metrik fəzası verilmişdir. Əgər bu fəzadan götürülmüş istənilən fundamental ardıcıllıq yığılan olarsa, bu fəzaya tam metrik fəza deyilir.
metrik fəzası verilmişdir. Əgər bu fəzadan götürülmüş istənilən fundamental ardıcıllıq yığılan olarsa, bu fəzaya tam metrik fəza deyilir.
Bəzi ədəbiyyatlarda tam metrik fəzaya dolu metrik fəza da deyilir.
Misal :  parçasında təyin olunmuş kəsilməz funksiyalar sinfi
parçasında təyin olunmuş kəsilməz funksiyalar sinfi

normasına görə tam metrik fəzadır. Doğrudan da istənilən fundamental 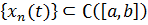 ardıcıllığı götürək. Onda tərifə əsasən
ardıcıllığı götürək. Onda tərifə əsasən  ədədinə görə
ədədinə görə  nömrəsi var ki,
nömrəsi var ki,  və
və  üçün
üçün

olar. Deməli, (1) şərti müntəzəm olaraq ödənilir. Aydındır ki, hər bir qeyd olunmuş 
 ədədi ardıcıllığı fundamentaldır. Onda ədədi ardıcıllıqlar üçün məlum olan Koşi meyarına əsasən, hər bir qeyd olunmuş
ədədi ardıcıllığı fundamentaldır. Onda ədədi ardıcıllıqlar üçün məlum olan Koşi meyarına əsasən, hər bir qeyd olunmuş 
 ardıcıllığı yığılan olar.
ardıcıllığı yığılan olar.
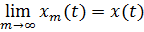
işarə edək. (1) şərtində  olduqda limitə keçsək, alarıq ki,
olduqda limitə keçsək, alarıq ki,  ədədinə görə
ədədinə görə  nömrəsi var ki,
nömrəsi var ki,  və
və  üçün
üçün  olar. Bu isə o deməkdir ki,
olar. Bu isə o deməkdir ki,  funksional ardıcıllığı x(t) funksiyasına müntəzəm yığılır. Onda
funksional ardıcıllığı x(t) funksiyasına müntəzəm yığılır. Onda 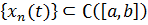 olduğundan
olduğundan  olar. Deməli,
olar. Deməli,  -də hər bir fundamental ardıcıllıq yığılandır. Bu isə o deməkdir ki,
-də hər bir fundamental ardıcıllıq yığılandır. Bu isə o deməkdir ki,  tam metrik fəzadır.
tam metrik fəzadır.
MÜHAZİRƏ 6.NORMALLAŞMIŞ FƏZA
Tutaq ki, L xətti fəzası verilmişdir və L fəzasında həqiqi ədədlər çoxluğuna təsir edən  funksiyası(funksionalı) aşağıdakı şərtləri ödəyir:
funksiyası(funksionalı) aşağıdakı şərtləri ödəyir:
1)  üçün
üçün 
2) 
3)  Onda p funksionalı L fəzasında norma adlanır. Norma daxil edilmiş fəzaya normallaşmış fəza deyilir. Hər bir
Onda p funksionalı L fəzasında norma adlanır. Norma daxil edilmiş fəzaya normallaşmış fəza deyilir. Hər bir  elementinin norması
elementinin norması  kimi işarə olunur.
kimi işarə olunur.
Hər bir normallaşmış fəza metrik fəzadır. Doğrudan da, bunu göstərmək üçün metrikanı  kimi daxil etmək kifayətdir.
kimi daxil etmək kifayətdir.
Misal :  ölçülü Evklid fəzasında hər bir ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
ölçülü Evklid fəzasında hər bir ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  nöqtələrinin normasını
nöqtələrinin normasını
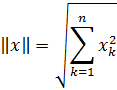
kimi daxil etmək olar. Aydındır ki, bu cür daxil olunmuş norma normanın əsas xassələrini ödəyir.
Məlumdur ki, xətti fəzanın altfəzası dedikdə toplama və ədədə vurma əməlinə görə qapalı olan altçoxluq başa düşülür.
Tutaq ki, L normallaşmış fəzası verilmişdir. Əgər  çoxluğu L xətti fəzasının altfəzası və L0 altfəzası qapalı çoxluq olarsa, L0 çoxluğuna L
çoxluğu L xətti fəzasının altfəzası və L0 altfəzası qapalı çoxluq olarsa, L0 çoxluğuna L
normallaşmış fəzasının altfəzası deyilir.
Qeyd edək ki, hər bir sonlu ölçülü normallaşmış fəzada xətti fəzanın istənilən altfəzası qapalı çoxluq olur. Lakin sonsuz ölçülü fəzada bu doğru olmaya da bilər. Məs:  fəzasında normanı
fəzasında normanı

kimi daxil edək və  parçasında təyin olunmuş bütün çoxhədlilər çoxluğunu
parçasında təyin olunmuş bütün çoxhədlilər çoxluğunu  ilə işarə edək. Aydındır ki,
ilə işarə edək. Aydındır ki, 
 xəti fəzasının altfəzasıdır. Lakin normallaşmış fəza kimi
xəti fəzasının altfəzasıdır. Lakin normallaşmış fəza kimi 
 -in altfəzası deyil, çünki,
-in altfəzası deyil, çünki,  -in qapanması
-in qapanması  -dən daha geniş olan
-dən daha geniş olan  çoxluğuna bərabərdir, yəni,
çoxluğuna bərabərdir, yəni,  qapalı çoxluq deyil.
qapalı çoxluq deyil.
Tam normallaşmış fəzaya Banax fəzası və ya B fəzası deyilir.
MÜHAZİRƏ 7.EVKLİD FƏZASI
Tutaq ki, L xətti fəzası verilmişdir və  elementləri cütünə
elementləri cütünə 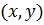 kimi işarə olunan yeganə həqiqi ədəd qarşı qoyan funksional aşağıdakı xassələri ödəyir:
kimi işarə olunan yeganə həqiqi ədəd qarşı qoyan funksional aşağıdakı xassələri ödəyir:
1) 
2) 
3) 
4) 
Onda deyirlər ki, L fəzasında skalyar hasil təyin olunmuşdur.
Skalyar hasil təyin olunan xətti fəzaya Evklid fəzası deyilir. Daha doğrusu Evklid fəzası dedikdə xətti fəza və bu fəzada təyin olunmuş skalyar hasil başa düşülür.
 ədədi və
ədədi və  elementləri götürək. Aydındır ki, skalyar hasilin məlum olan xassələrinə əsasən
elementləri götürək. Aydındır ki, skalyar hasilin məlum olan xassələrinə əsasən

Əgər  elementləri xətti asılı deyilsə
elementləri xətti asılı deyilsə  olar. Digər tərəfdən
olar. Digər tərəfdən  a nəzərən kvadratik üçhədli olduğundan məlumdur ki,
a nəzərən kvadratik üçhədli olduğundan məlumdur ki,  şərtindən alırıq ki,
şərtindən alırıq ki,  həqiqi kökləri yoxdur və deməli, diskriminant mənfidir:
həqiqi kökləri yoxdur və deməli, diskriminant mənfidir:


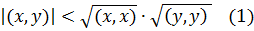
Asanlıqla yoxlamaq olar ki, hər bir Evklid fəzası normallaşmış fəzadır, bunun üçün 
Normanın bu cür daxil olunmasını (1) bərabərsizliyində nəzərə alsaq, xətti asılı olmayan elementlər üçün
 olduğunu alarıq.
olduğunu alarıq.
Aydındır ki, x və y elementləri xətti asılı olarsa, (2) bərabərsizliyi bərabərliyə çevrilər. Onda  elementləri üçün
elementləri üçün
 olduğunu alarıq.
olduğunu alarıq.
(3) bərabərsizliyi Koşi-Bunyakovski bərabərsizliyi adlanır. Əgər  olarsa, x və y elementlərinə ortoqonal elementlər deyilir.
olarsa, x və y elementlərinə ortoqonal elementlər deyilir.
MÜHAZİRƏ 8.ORTOQONAL VƏ ORTONORMAL SİSTEMLƏR.BAZİS ANLAYIŞI.
Tutaq ki, L Evklid fəzası və bu fəzadan götürülmüş  elementlər sistemi verilmişdir. Əgər
elementlər sistemi verilmişdir. Əgər  olduqda
olduqda  =0 olarsa,
=0 olarsa,  sistemi ortoqonal sistem adlanır. Əgər
sistemi ortoqonal sistem adlanır. Əgər

olarsa,  sistemi ortonormal sistem adlanır.
sistemi ortonormal sistem adlanır.
Göstərmək olar ki, ortoqonal sistem xətti asılı deyil. Doğrudan da əgər
 olarsa, bu ayrılışın hər tərəfinin
olarsa, bu ayrılışın hər tərəfinin  skalyar hasilinə baxsaq
skalyar hasilinə baxsaq 


 olduğunu alarıq.
olduğunu alarıq.
Tutaq ki, L Evklid fəzasında  ortoqonal sistemi verilmişdir. Əgər
ortoqonal sistemi verilmişdir. Əgər  sisteminin elementlərinin xətti kombinasiyaları çoxluğunun qapanması bütün L fəzasını verərsə, yəni
sisteminin elementlərinin xətti kombinasiyaları çoxluğunun qapanması bütün L fəzasını verərsə, yəni  sistemi L fəzasında sıx olarsa, bu sistemə L fəzasında ortoqonal bazis deyilir. Əgər bu zaman
sistemi L fəzasında sıx olarsa, bu sistemə L fəzasında ortoqonal bazis deyilir. Əgər bu zaman  sistemi ortonormal olarsa, bu sistem ortonormal bazis adlanır.
sistemi ortonormal olarsa, bu sistem ortonormal bazis adlanır.
Misal : Rnfəzasında


--------------------

 ortonormal sistemi bazis təşkil edir. Doğrudan da
ortonormal sistemi bazis təşkil edir. Doğrudan da  fəzasının hər bir x elementini
fəzasının hər bir x elementini  şəklində göstərmək mümkündür.
şəklində göstərmək mümkündür.
Əgər L Evklid fəzasında hesabi sıx çoxluq varsa, bu fəza Seperabel-Evklid fəzası adlanır. Məsələn, l2 fəzasında


-----------------------

sistemi ortonormal bazis təşkil edir və bu bazisin elementləri hesabi sayda olduğundan l2 fəzası Seperabel-Evklid fəzasıdır.
Teorem : Tutaq ki, L Evklid fəzasında xətti asılı olmayan  elementlər sistemi verilmişdir. Onda L fəzasında elə ortonormal
elementlər sistemi verilmişdir. Onda L fəzasında elə ortonormal  sistemi var ki,
sistemi var ki,
1). 
2).  olar.
olar.
Isbatı : Verilmiş  sisteminə uyğun olaraq
sisteminə uyğun olaraq  sistemini induktiv olaraq aşağıdakı qaydada quraq:
sistemini induktiv olaraq aşağıdakı qaydada quraq:
 götürək. Belə ki,
götürək. Belə ki, 

Tutaq ki,  natural ədədləri üçün
natural ədədləri üçün  -ları təyin etmişik. Induktiv olaraq
-ları təyin etmişik. Induktiv olaraq  təyin edək. Onda
təyin edək. Onda

Aydındır ki, 

kimi təyin edək. Göründüyü kimi, bu qayda ilə qurulan sistem ortonormaldır və qeyd olunan xassələri ödəyir. Teorem isbat olundu.
MÜHAZİRƏ 9.EVKLİD FƏZASINDA FURYE SIRASI
Tutaq ki, L Evklid fəzası və bu fəzada  ortonormal sistemi verilmişdir.
ortonormal sistemi verilmişdir.  elementi götürək və
elementi götürək və

sırasını düzəldək, burada 
(1) sırasına f elementinin Furye sırasına ayrılışı,  ədədlərinə
ədədlərinə
isə, f elementinin Furye sırasının əmsalları deyilir.
Indi isə, (1) sırasının yığılan olub-olmamasını, yığılandırsa, bu sıranın cəminin f elementinə bərabər olub-olmamasını araşdıraq.
 ədədlərini elə seçək ki,
ədədlərini elə seçək ki,

sırası ilə f elementi arasındakı məsafə minimal olsun.

işarə edək. Aydındır ki,

 (3) olar.
(3) olar.
Göründüyü kimi  ifadəsi minimal qiymətini
ifadəsi minimal qiymətini  olduqda alır. Deməli, (2) şəklində olan sıralardan məsafəcə f elementinə ən yaxın olan sıra f elementinin Furye sırasıdır. Bu zaman
olduqda alır. Deməli, (2) şəklində olan sıralardan məsafəcə f elementinə ən yaxın olan sıra f elementinin Furye sırasıdır. Bu zaman


olduğunu alarıq. (5) bərabərsizliyi istənilən n natural ədədi üçün doğru olduğundan və bu bərabərsizliyin sağ tərəfi n-dən asılı olmadığına görə

(6) bərabərsizliyi Bessel bərabərsizliyi adlanır. Bu bərabərsizlikdən aydındır ki, Furye əmsallarının kvadratından düzəldilmiş sıra yığılandır.
Tərif : Tutaq ki, L Evklid fəzasında  ortonormal sistemi verilmişdir. Əgər
ortonormal sistemi verilmişdir. Əgər  elementi üçün
elementi üçün

(7) ortonormal sistemi L Evklid fəzasında qapalı sistem adlanır, burada 
(8) bərabərliyi Parseval bərabərliyi adlanır.
(4) bərabərliyindən aydındır ki, əgər (7) sistemi qapalı olarsa, yəni Parseval bərabərliyi ödənərsə,

olar. Bu isə o deməkdir ki, bu zaman, yəni Parseval bərabərliyi ödəndikdə f elementinin Furye sırası bu elementin özünə yığılır.
Teorem : Seperabel-Evklid fəzasında ortonormal sistemin qapalı olması üçün zəruri və kafi şərt bu sistemin tam(dolu) olmasıdır.
Isbatı : (zərurilik) Tutaq ki,  sistemi L Seperabel-Evklid fəzasında qapalıdır. Onda aydındır ki, bu zaman
sistemi L Seperabel-Evklid fəzasında qapalıdır. Onda aydındır ki, bu zaman  elementinin Furye sırası f elementinin özünə yığılır. Daha doğrusu, f elementinə (7) sisteminin elementlərinin xətti kombinasiyaları ilə yaxınlaşmaq mümkündür. Bu isə o deməkdir ki, (7) sistemi dolu sistem təşkil edir.
elementinin Furye sırası f elementinin özünə yığılır. Daha doğrusu, f elementinə (7) sisteminin elementlərinin xətti kombinasiyaları ilə yaxınlaşmaq mümkündür. Bu isə o deməkdir ki, (7) sistemi dolu sistem təşkil edir.
(kafilik): Tutaq ki, (7) sistemi dolu sistemdir. Onda tərifə əsasən (7) sisteminin elementlərinin xətti kombinasiyaları vasitəsilə f elementinə yaxınlaşmaq mümkündür(yəni, aproksimasiya etmək). (7) sisteminin elementlərinin xətti kombinasiyalarından f -ə ən yaxşı aproksimasiya olunan f elementinin Furye sırasıdır. Deməli, bu zaman f elementinin Furye sırası bu elementin özünə yığılır. Bu isə o deməkdir ki, Parseval bərabərliyi ödənir və deməli, (7) sistemi qapalıdır. Teorem isbat olundu.
Biz bu mövzuda elementin ortonormal sistem üzrə Furye sırasına ayrılışını göstərdik. Indi isə elementin ortoqonal sistem üzrə Furye sırasına ayrılışını yazaq:
Tutaq ki, L Evklid fəzası və bu fəzada  ortoqonal sistemi verilmişdir.
ortoqonal sistemi verilmişdir.

Aydındır ki,  olduqda
olduqda


Deməli, bu qaydayla qurulan  sistemi ortonormal sistem olar.
sistemi ortonormal sistem olar.
 elementi götürək və
elementi götürək və  işarə edək. Onda məlumdur ki, f elementinin Furye sırasına ayrılışı
işarə edək. Onda məlumdur ki, f elementinin Furye sırasına ayrılışı


(9) sırası f elementinin ortoqonal sistem üzrə Furye sırasına ayrılışı adlanır.
MÜHAZİRƏ 10.TAM EVKLİD FƏZASI. RİSS-FİŞER TEOREMİ
Tutaq ki, L Evklid fəzası verilmişdir. Əgər bu fəza 
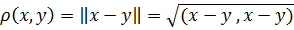 metrikasına nəzərən tam fəza olarsa, L fəzasına tam Evklid fəzası deyilir.
metrikasına nəzərən tam fəza olarsa, L fəzasına tam Evklid fəzası deyilir.
Tutaq ki, L tam Seperabel-Evklid fəzası və bu fəzadan götürülmüş  ortonormal sistemi verilmişdir. Aydındır ki,
ortonormal sistemi verilmişdir. Aydındır ki, 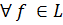 elementi üçün bu elementin Furye sırasına yığılan olması üçün zəruri və kafi şərt Bessel bərabərsizliyinə əsasən
elementi üçün bu elementin Furye sırasına yığılan olması üçün zəruri və kafi şərt Bessel bərabərsizliyinə əsasən  elementinin
elementinin  Furye əmsallarından düzəldilmiş
Furye əmsallarından düzəldilmiş

sırasının yığılan olmasıdır. Aşağıdakı teorem onu göstərir ki, bu şərt həm də kafidir.
Teorem 1:(Riss-Fişer) Tutaq ki, L tam Evklid fəzası və bu fəzadan götürülmüş  ortonormal sistemi verilmişdir. Onda
ortonormal sistemi verilmişdir. Onda

şərtini ödəyən  ədədləri üçün
ədədləri üçün  elementi var ki,
elementi var ki, 

Isbatı :





Bu isə o deməkdir ki, 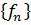 ardıcıllığı fundamentaldır. L fəzası tam olduğundan hər bir fundamental ardıcıllıq yığılandır və deməli,
ardıcıllığı fundamentaldır. L fəzası tam olduğundan hər bir fundamental ardıcıllıq yığılandır və deməli, 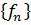 ardıcıllığı yığılandır.
ardıcıllığı yığılandır.

Aydındır ki,  olduqda
olduqda 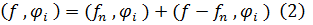 və Koşi-Bunyakovski bərabərsizliyinə əsasən,
və Koşi-Bunyakovski bərabərsizliyinə əsasən,

olduqda (2) bərabərliyində limitə keçsək,
 alarıq.
alarıq.

Bu bərabərlikdə 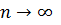 olduqda limitə keçsək,
olduqda limitə keçsək,

Teorem isbat olundu.
Isbatsız olaraq aşağıdakı teoremi qeyd edək
Teorem 2: Tutaq ki , L tam Seperabel Evklid fəzası və bu fəzadan götürülmüş  ortonormal sistemi verilmişdir.
ortonormal sistemi verilmişdir.  sisteminin qapalı olması üçün zəruri və kafi şərt bu sistemin hər bir elementinə ortoqonal olan L fəzasından götürülmüş sıfır elementin olmamasıdır.
sisteminin qapalı olması üçün zəruri və kafi şərt bu sistemin hər bir elementinə ortoqonal olan L fəzasından götürülmüş sıfır elementin olmamasıdır.
MÜHAZİRƏ 11.HİLBERT FƏZASI. HİLBERT FƏZASININ İZOMORFLUĞU
Tərif 1: Tam sonsuz ölçülü Evklid fəzası Hilbert fəzasıdır.
Biz bu mövzuda adətən Seperabel- Hilbert fəzasından danışacağıq:
Tərif 2: Tutaq ki, L və L* Evklid fəzaları arasında qarşılıqlı birqiymətli uyğunluq var və 
1) 
2) 
3) 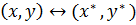 şərti ödənir. Onda L və
şərti ödənir. Onda L və  fəzaları bir-birinə izomorf olan fəzalar adlanır.
fəzaları bir-birinə izomorf olan fəzalar adlanır.
Aydındır ki, sonlu ölçülü Evklid fəzaları çoxluğunda eyniölçülü olan Evklid fəzaları bir-birinə izomorfdur. Deməli,  ölçülü Evklid fəzası
ölçülü Evklid fəzası  fəzasına izomorfdur. Lakin sonsuz ölçülü Evklid fəzalarında bu fakt doğru olmaya da bilər. Məsələn,
fəzasına izomorfdur. Lakin sonsuz ölçülü Evklid fəzalarında bu fakt doğru olmaya da bilər. Məsələn,  Evklid fəzaları sonsuz ölçülüdür, lakin izomorf deyillər. Çünki ən azı
Evklid fəzaları sonsuz ölçülüdür, lakin izomorf deyillər. Çünki ən azı  tam Evklid fəzasıdır, lakin,
tam Evklid fəzasıdır, lakin,  Evklid fəzası tam deyil.
Evklid fəzası tam deyil.
Misal :  fəzası Seperabel- Hilbert fəzasıdır.
fəzası Seperabel- Hilbert fəzasıdır.
Teorem : İstənilən iki Seperabel-Hilbert fəzaları bir-birinə izomorfdur.
Isbatı : Əvvəlcə göstərək ki,  Seperabel-Hilbert fəzası
Seperabel-Hilbert fəzası  fəzasına izomorfdur.
fəzasına izomorfdur.  fəzasında
fəzasında  hər hansı
hər hansı  ortonormal sistemi götürək. Aydındır ki,
ortonormal sistemi götürək. Aydındır ki,  fəzasından götürülmüş
fəzasından götürülmüş  elementinə qarşı bu elementin
elementinə qarşı bu elementin  Furye əmsallarını uyğun qoymaq olar. Bessel bərabərsizliyinə əsasən,
Furye əmsallarını uyğun qoymaq olar. Bessel bərabərsizliyinə əsasən,

 elementi götürək. Bu zaman
elementi götürək. Bu zaman

Onda Riss-Fişer teoreminə əsasən,  elementi var ki,
elementi var ki,  ədədləri f elementinin Furye əmsalları olar. Bu qaydayla biz
ədədləri f elementinin Furye əmsalları olar. Bu qaydayla biz  fəzaları arasında qarşılıqlı birqiymətli uyğunluq yaratmış olarıq:
fəzaları arasında qarşılıqlı birqiymətli uyğunluq yaratmış olarıq:
Tutaq ki, 


Burada  elementinin,
elementinin,  elementinin Furye əmsallarıdır. Onda asanlıqla göstərmək olar ki,
elementinin Furye əmsallarıdır. Onda asanlıqla göstərmək olar ki,



Deməli, istənilən Seperabel-Hilbert fəzası  fəzasına izomorfdur. Buradan isə alarıq ki, istənilən iki Seperabel-Hilbert fəzası bir-birinə izomorfdur. Teorem isbat olundu.
fəzasına izomorfdur. Buradan isə alarıq ki, istənilən iki Seperabel-Hilbert fəzası bir-birinə izomorfdur. Teorem isbat olundu.
MÜHAZİRƏ 12.XƏTTİ FUNKSİONAL ANLAYIŞI
Tutaq ki, L xətti fəzası verilmişdir. L fəzasında həqiqi ədədlər və ya kompleks ədədlər çoxluğuna təsir edən inikas funksional adlanır.
Tərif 1: Tutaq ki, L xətti fəzasında təyin olunmuş f funksionalı verilmişdir. Əgər  olarsa, f funksionalına additiv funksional deyilir.
olarsa, f funksionalına additiv funksional deyilir.
Tərif 2: Əgər  nöqtəsi üçün
nöqtəsi üçün  olarsa, f funksionalına bircins funksional deyilir.
olarsa, f funksionalına bircins funksional deyilir.
Tərif 3: Həm additiv, həm dəbircins olan funksionala xətti funksional deyilir.
Misal :  fəzasından götürülmüş
fəzasından götürülmüş  funksiyasına qarşı
funksiyasına qarşı
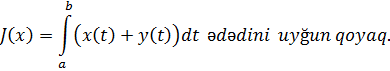
Aydındır ki, bu funksional xəttidir. Doğrudan da
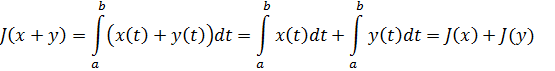

Tərif 4: Əgər  elementi üçün
elementi üçün  olarsa, f funksionalına qoşma bircins funksional deyilir.
olarsa, f funksionalına qoşma bircins funksional deyilir.
Tərif 5: Additiv və qoşma-bircins olan funksionala qoşma-xətti və ya yarımxətti funksional deyilir.
Tutaq ki, L xətti fəzasında təyin olunmuş f xətti funksionalı verilmişdir.  tənliyinin köklərinin əmələ gətirdiyi çoxluğa f funksionalının nüvəsi deyilir və Kerf kimi işarə olunur. Aydındır ki,
tənliyinin köklərinin əmələ gətirdiyi çoxluğa f funksionalının nüvəsi deyilir və Kerf kimi işarə olunur. Aydındır ki,  və Kerf çoxluğu boş deyil, çünki, ən azı
və Kerf çoxluğu boş deyil, çünki, ən azı  tənliyinin trivial həlli var. Əgər
tənliyinin trivial həlli var. Əgər  olar. Bu isə o deməkdir ki,
olar. Bu isə o deməkdir ki, 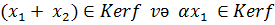 olar. Daha doğrusu Kerf çoxluğu L xətti fəzasının altfəzasıdır.
olar. Daha doğrusu Kerf çoxluğu L xətti fəzasının altfəzasıdır.
MÜHAZİRƏ 13.QABARIQ ÇOXLUQ VƏ QABARIQ FUNKSİONAL ANLAYIŞI
Tutaq ki, L xətti fəzası verilmişdir və 
 şəklində olan bütün mümkün nöqtələr çoxluğuna
şəklində olan bütün mümkün nöqtələr çoxluğuna  nöqtələrini birləşdirən parça deyilir.
nöqtələrini birləşdirən parça deyilir.
Tutaq ki,  çoxluğu verilmişdir və
çoxluğu verilmişdir və  çoxluğunun istənilən 2 nöqtəsini birləşdirən parça da
çoxluğunun istənilən 2 nöqtəsini birləşdirən parça da  çoxluğuna daxil olarsa, bu zaman həmin çoxluğa qabarıq çoxluq deyilir.
çoxluğuna daxil olarsa, bu zaman həmin çoxluğa qabarıq çoxluq deyilir.
Əgər  nöqtələrini birləşdirən parçadan bu nöqtələri atdıqdan sonra alınan çoxluğa
nöqtələrini birləşdirən parçadan bu nöqtələri atdıqdan sonra alınan çoxluğa 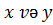 nöqtələrini birləşdirən açıq parça deyilir.
nöqtələrini birləşdirən açıq parça deyilir.
Tərif 1: Tutaq ki,  xətti fəzası və
xətti fəzası və  çoxluğu verilmişdir və
çoxluğu verilmişdir və  ədədi var ki,
ədədi var ki,  şərtini ödəyən
şərtini ödəyən  elementi üçün
elementi üçün  . Bütün bu cür
. Bütün bu cür  nöqtələri çoxluğuna
nöqtələri çoxluğuna  çoxluğunun nüvəsi deyilir.
çoxluğunun nüvəsi deyilir.
Tərif 2: Nüvəsi boş olmayan qabarıq çoxluğa qabarıq cisim deyilir.
Tərif 3: Tutaq ki,  xətti fəzası və bu fəzada təyin olunmuş
xətti fəzası və bu fəzada təyin olunmuş  funksionalı verilmişdir. Əgər
funksionalı verilmişdir. Əgər  elementləri və
elementləri və  ədədi üçün
ədədi üçün  olarsa,
olarsa,  funksionalına qabarıq funksional deyilir.
funksionalına qabarıq funksional deyilir.
Tərif 4:Tutaq ki,  elementi və
elementi və  ədədi üçün
ədədi üçün  şərti ödənilir. Onda p funksionalına müsbət bircins funksional deyilir.
şərti ödənilir. Onda p funksionalına müsbət bircins funksional deyilir.
Tərif 5: Qabarıq və müsbət bircins olan funksionala bircins qabarıq funksional deyilir.
Tutaq ki, L xətti fəzasında təyin olunmuş p bircins qabarıq funksionalı verilmişdir. Onda  elementlər
elementlər
Date: 2016-06-13; view: 140
| <== previous page | | | next page ==> |
| FUNKSİONAL ANALİZ | | | THE Grifburgh Empire |