FUNKSİONAL ANALİZ

MÜHAZİRƏ 1.XƏTTİ FƏZA ANLAYIŞI. XƏTTİ FƏZANIN ÖLÇÜSÜ

Tutaq ki,boş olmayan L çoxluğu aşağıdakı xassələri ödəyir:

I) elementlərinə qarşı bu elementlərin cəmi adlanan və x+y kimi işarə olunan elementi var ki, z=x+y

1) üçün x+y=y+z

2) üçün x+(y+t)=(x+y)+t

3) Sıfır adlanan və ?0? kimi işarə olunan elementi var ki, üçün x+0=x

4) 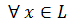elementi üçün bu elementin əksi adlanan və (-x) kimi işarə olunan elementi var ki, x+y=0 olar, burada y= -x

II) elementi və ədədi(həqiqi və ya kompleks) üçün ədədinin x elementinə hasili adlanan və kimi işarə olunan elementi var ki,

1)

2)

3)

4) olar. Onda L çoxluğuna xətti fəzadeyilir. Deməli, xətti fəza dedikdə toplama və ədədə vurma əməlinə görə qapalı olan çoxluq başa düşülür. Daha doğrusu, çoxluğun 2 elementinin cəmi də bu çoxluğa daxildirsə və çoxluğun elementinin ədədə hasili də bu çoxluğa daxildirsə, bu çoxluq xətti fəzaadlanır.

Tutaq ki, L və xətti fəzaları arasında qarşılıqlı birqiymətli uyğunluq yaratmaq mümkündür, belə ki, olduqda x+ y və ədədi üçün . Onda L və xətti fəzaları izomorf xətti fəzalaradlanır.

Tutaq ki, L xətti fəzası verilmişdir. Əgər elementləri üçün heç olmazsa biri sıfırdan fərqli olan ədədləri varsa ki, olsun. Onda elementləri xətti asılıadlanır. Əks halda ,yəni, bərabərliyi yalnız və yalnız olduqda doğru olarsa, elementlərinə xətti asılı olmayanelementlər deyilir.

Əgər L xətti fəzasının sayda xətti asılı olmayan elementləri varsa və (n+1) sayda elementləri xətti asılı olarsa, bu zaman n natural ədədi L fəzasının ölçüsüadlanır.

Tutaq ki, L xətti fəzası verilmişdir və . Əgər və ədədi üçün x+y və olarsa, çoxluğu L çoxluğunun alt fəzası adlanır.

n ölçülü xətti fəzanın xətti asılı olmayan n sayda elementlər sistemi bu xətti fəzanın bazisiadlanır.

MÜHAZİRƏ 2.METRİK FƏZA. İZOMETRİYA

Tutaq ki, X çoxluğu verilmişdir. Əgər elementlərinə qarşı yeganə həqiqi ədədi qarşı qoyan inikas aşağıdakı xassələri ödəyirsə, inikasına metrikadeyilir:

1)

2) s w:val="28"/><w:lang w:val="AZ-LATIN"/></w:rPr><m:t>y,x</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:fareast="Times New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="AZ-LATIN"/></w:rPr><m:t> (simmetriklik)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">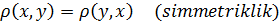

3)

Bu zaman deyirlər ki, X çoxluğunda metrika təyin olunmuşdur.

Tutaq ki, X çoxluğunda metrikası verilmişdir. Bu zaman (x, ) cütü metrik fəzaadlanır.

Misal 1: Tutaq ki, hər hansı X çoxluğu verilmişdir. Bu çoxluqda həmişə aşağıdakı kimi metrika təyin etmək mümkündür.

Misal 2: həqiqi ədədlər çoxluğunu götürək

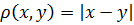kimi metrika daxil olunur

Misal 3: parçasında təyin olunmuş kəsilməz funksiyalar çoxluğunda yəni, çoxluğunda metrikanı

kimi daxil etmək olar. Doğrudan da

1) üçün f(x)=g(x)

2) üçün olduğundan s w:val="28"/><w:lang w:val="AZ-LATIN"/></w:rPr><m:t>g,f</m:t></m:r></m:e></m:d></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> olar.

3) funksiyaları üçün olduğundan bu bərabərsizliyin hər iki tərəfindən maksimuma keçsək, alarıq.

Bəzi fəzaların metrik fəza olmasını göstərmək üçün aşağıdakı bərabərsizliklərdən geniş istifadə olunur:

Date: 2016-06-13; view: 6