
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
When 8is sufficiently small, the first term is the smaller of the two, and it is well approximated by the expression 4 page
Proof. We shall in fact prove a slightly sharper version of this result by formulating the sense in which the game must be generic. Given an í-person game G on the finite strategy space X = |~[ X„ let B~l(Xi) denote the set of all probability mixtures p-i 6 Ä-, = Ï,#1 MXj) s110'1 that x, is a best reply to We say that G is nondegenerate in best replies
(NDBR) if for every i and every x, e X„ either B~'(x,) is empty or it contains a nonempty subset that is open in the relative topology of Ä _,. The set of NDBR games is open and dense in the space R"|X|, so NDBR is a generic property.
Given a positive integer s, we say that the probability distribution p- G ä, has precision s if sp,(x,) is integer for all x, e X,. We shall denote the set of all such distributions by Ä ■. For each subset Y, of X„ let Ä*( Y,) denote the set of distributions p; e Ä- such that /?,(*,) > 0 implies x, e Y,. For each positive integer s, let BRj(X_,) be the set of pure-strategy best replies by i to some product distribution p., e Ä1 ,(X_,) = f],^, A;(X,). Similarly ÂÖ (Y_,) denotes the set of all best replies by i to some product distribution ˆ Ä1 ,(Y_;).
For each product set Y and player i, define the mapping 0,(Y) = Y, U BRj(Y-j), and let p(Y) = Ï ft(Y). Similarly for each integer s > 1 let
fif(Y) = Yi U BR*(Y_,) and 0S(Y) = f] pf(Y).
Clearly, p*(Y) ñ p(Y) for every product set Y. We claim that if G is NDBR, then 0S(Y) = 0(Y) for all sufficiently large s. To establish this claim, suppose that x, e Ä(Ó). If x, e Y„ then obviously .v, e Pf(Y). If Xt 6 Pi(Y)-Y„ then Â~ã(õ,) Ô È, so by hypothesis, the set of distributions p-i = ]-I;7s, Pito which .v, is a best reply contains a nonempty open subset of Ä_,. Hence there exists an integer s,(.r,, Y_,) such that äã, is a best reply to some distribution pi, = e AS_,(Y_,) for alls > Y_,). Since
there are n strategy sets, all of which are finite, it follows that there is an integer s(Y) such that ps(Y) = p(Y) for all s > s(Y). Since the number of product sets Y is finite, it follows that there is an integer s* such that PHY) = p(Y) for all s > s* and all product sets Y, as claimed.
Now consider the process P'" f 0. We shall show that ifs is large enough and s/m is small enough, the spans of the recurrent classes correspond one to one with the minimal curb sets of G. We begin by choosing s large enough that ps = p. Then we choose m such that m > s|X|.
| (À.18) |
Fix a recurrent class E* of P"' s 0, and choose any h° e Ejt as the initial state. We shall show that the span of Ejt, S(E*), is a minimal curb set. As in the proof of theorem 7.1 above, there is a positive probability of reaching a state h] in which the most recent s entries involve a repetition of some fixed x* e X. Note that It1 ˆ Ek, because Ek is a recurrent class. Let pli] denote the /-fold iteration of p and consider the nested sequence
!**} ñ /3((õ*}) ñ 0,2,({.v*}) ñ ... ñ ^({.ã')) ñ
Since X is finite, there exists some point at which this sequence becomes constant, say, 0<"({x')) = 0('+1)({x*}) = Ó*. By construction, Ó* is a curb set.
Assume that the above sequence is nontrivial, that is, £((x*)) Ô {õ*}. (If (f(x*) = {.v*}, then the following argument is not needed.) There is a positive probability that, beginning after the history li\ some x1 e 0({x*)) - |x*} will be chosen for the next s periods. Call the resulting history lr. Then there is a positive probability that x2 e f)({x' |) - (x*. x1) will be chosen for the next s periods, and so forth. Continuing in this fashion, we eventually obtain a history hk such that all members of /j(|x*)), including the original X*, appear at least s times. All we need assume is that m is large enough so that the original s repetitions of x* have not been forgotten. This is clearly assured if m > s|X|. Continuing this argument, we see that there is a positive probability of eventually obtaining a history h' in which all members of Ó* = /^({õ*|) appear at least s times within the last s|Y*| periods. In particular, S(/i*) contains Ó, which by construction is a curb set.
We claim that Ó* is in fact a minimal curb set. To establish this, let Z* be a minimal curb set contained in Y*, and choose 2* e Z*. Beginning with the history h" already constructed, there is a positive probability that 2* will be chosen for the next s periods. After this, there is a positive probability that only members of /3({z*)) will be chosen, or members of fi(2)({2*}), or members of ^(3>(|z*)), and so on. This happens if agents always draw samples from the "new" part of the history that follows It*, which they will do with positive probability.
The sequence /J'*4(2*}) eventually becomes constant with value Z* because Z* is a minimal curb set. Moreover, the part of the history before the s-fold repetition of x* will be forgotten within m periods. Thus there is a positive probability of obtaining a history //** such that S(h**) ñ Z*. From such a history the process Pm s0 can never generate a history with members that are not in Z* because Z* is a curb set.
Since the chain of events that led to //" began with a state in Ejt, which is a recurrent class, h" is also in E/t; moreover, every state in Ek is reachable from /1". It follows that Ó* ñ S(Ek) ñ Z*, from which we conclude that Y* = S(Ek) = Z* as claimed.
Conversely, we must show that if Y* is a minimal curb set, then Y* = S(Ek) for some recurrent class Ek of Pm s0. Choose an initial history h° that involves only strategies in Ó*. Starting at li°, the process P" s0 generates histories that involve no strategies that lie outside of S(h°), fi(S(//0)). fi(2)(S(h0)), and so on. Since Y* is a curb set, all of these strategies must occur in Ó*. With probability one the process eventually enters a recurrent class, say £;. It follows that S(Ek) ñ Ó*. Since ó* is a minimal curb set, the earlier part of the argument shows that 5(£;) = Ó*. This establishes the one-to-one correspondence between minimal curb sets and the recurrent classes of Pm s-°. Theorem 7.2 now follows immediately from theorem 3.1.
remark. If G is degenerate in best replies, the theorem can fail. Consider the following example:
À Â Ñ D
|
In this game, ñ is a best reply to A, A is a best reply to ÿ, ÿ is a best reply to C, and Ñ is a best reply to c. Hence any curb set that involves one or more of (À. Ñ, ÿ, ñ) must involve all of them. Hence it must involve b, because b is a best reply to the probability mixture 1/(1 + ,/2) on A and ,/2/(1 + y/2) on C. Hence it must involve B, because  is a best reply to b. However, d is the unique best reply to B, and D is the unique best reply to d. From this it follows that every curb set contains (d, D). Since the latter is a minimal curb set (a strict Nash equilibrium), we conclude that ((d. D)) is the unique minimal curb set. However, {(d. D)) does not correspond to the unique recurrent class under adaptive learning.
To see why, consider any probability mixture (q,\. qn. qc. qD) over column's strategies. It can be checked that strategy b is a best reply (by row) if and only if qB = 0, qc = (J2)qA, qD = 1 - (1 + s/2)qA, and â a > 1/(2 + ^2), in which case ÿ and ñ are also best replies. In this situation at least one of qA and qc must be an irrational number. In adaptive learning, however, row responds to sample frequencies, which can only be rational numbers. It follows that, when s — 0, row will never choose b as a best reply to sample information no matter how large s is. Thus, with finite samples, the unperturbed process has two recurrent classes: one with span {ÿ. ñ) æ (À. Ñ), the other with span {(d. D)). Hence theorem 7.2 does not hold for this (nongeneric) two person game.
Theorem 9.1. Let G be a two-person pure coordination game, and let pm s * be adaptive play. If s/m is sufficiently small, every stochastically stable state is a convention; moreover, if s is sufficiently large, every such convention is efficient and approximately maximin in the sense that its welfare index is at least (iv+ - or)/(l + a), where
a = w~( 1 - (ãî+)2)/(1 + w~)(w+ + w~). (A.19)
Proof. Let G be a pure coordination game with diagonal payoffs (ar bj) > (0,0). 1 < j < K, and off-diagonal payoffs (0, 0). Assume that the payoffs have been normalized so that max, ÿó = max,b; = 1. The welfare index of the yth coordination equilibrium is defined to be W; = ÿ, ë b,, and a>+ = maxy Wj. We also recall that a~ = min |ÿ,:Üó = 1}, b~ = min [bj-.aj = 1), and w~ = a~ v b~.
Let P' = p"' Sf denote adaptive learning with parameters m, s, and e. Theorem 7.1 shows that if s/m is sufficiently small, the only recurrent classes of the unperturbed process P"KS-° are the Ê conventions h\. //2,... Jik corresponding to the Ê coordination equilibria. From (9.5) we know that for every two conventions lij and hk, the resistance to the transition hj —► hk is
r)k = \srjk1 where rjk = aj/ia, + ak) ë bt/(bj + bk). (A.20)
It will be convenient to do calculations in terms of the "reduced resistances" rjk, which are more or less proportional to the actual resistances when s is large.
Construct a directed graph with Ê vertices, one for each of the conventions [h].li2 Iik). Let the weight on the directed edge hj —> hk
be the reduced resistance rjk. Assume that hj is stochastically stable for some value of s. By theorem 3.1, the stochastic potential computed according to the resistances is minimized at hj. If s is large enough, the stochastic potential computed according to the reduced resistances rjk must be minimized at hj also, that is, there is a j-tree T, such that r(Tj) < r(T) for all rooted trees T. (In general, r(T) denotes the sum of reduced resistances of all directed edges in the set T.) We need to show that this implies
Wj > (w+ -«)/(! +ff).
e
|
| tei* |
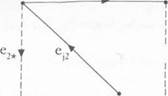
| Figure A.6. The dashed edges are replaced by the solid edges to form a 1 -tree. |
Clearly this follows if zvj — zu+. Hence we may assume that zv, < iv+, that is, j is not a maximin equilibrium. (For brevity we shall refer to the equilibria by their indices.) Without loss of generality, let us suppose that equilibrium 1 is maximin (zvj = zv+), j > 2, and in equilibrium / the row players are "worse off" than the column players: Wj = aó < by.
Let /' be an equilibrium with payoffs fly = 1 and bf = b~. Since <ij < zv+ < 1, j and f must be distinct. Assume for the moment that /' Ô 1. (Later we shall dispose of the case / = 1, that is, b~ = w+.) Without loss of generality, let j' = 2: thus a2 = 1 and b2=b'.
| appendix |
Fix a least resistant /-tree Òó. Since j -ô 1.2, there is a unique edge e\. in Òó exiting from vertex 1, and a unique edge e2- exiting from vertex 2 (see Figure A.6).
| (A.21) |
| (A.22) |
Delete the edges e\- and e2- from Tj and add the edges e/2 from j to 2 and e2\ from 2 to 1. This results in a 1-tree T\. (This is also true ifey and e2■ point toward the same vertex, or if e2- is the same as e2\.) We know that r(Tj) < r(Ti), so
Ã]. + r2- < rj2 + r2i.
Let us eval uate the four reduced resistances in this expression. By (A.20),
* Ãóã = À//(À/ + "2) A bj/(bj + b2) = 0,1(0, + 1) Ë bj/(bj + b~).
Since zvj = ÿ; < bj by hypothesis, it follows that
Ã12 = ZVj/(ZVj + 1).
By (A.20), the minimum reduced resistance from 1 to any other vertex is
min [ci\/(ci\ + ak) ë b\/(bx + bk)). ê
Since 1 is a maximin equilibrium, we have Ï\, b\ > w+. Moreover, ak, bk < 1 for all k. Hence
min + ak) ë b\/(b\ + bk)) > w+/(w+ + 1).
ê
It follows that
rj. > w+/(w+ + 1). (A.23)
| (A.24) |
A similar argument shows that
r2. > b~/(b~ + 1).
Finally, since alr b\ > w+, we have
r2i = a2/(a2 + <?i) ëÜ2/(Ü2 + bi) < 1/(1+ w+) ë b~/(b~ + a>+).
and in particular,
r2\ < b~/{b~ + w+). (A.25)
Combining (A.22)-(A.25) yields the inequality
iv+ b~ Wj b~
------------ 1--------- <-------- i---- 1------------ .
w+ + 1 b~ + 1 ~ Wj + 1 b~ + w+
After some algebraic manipulation, this leads to the equivalent expression
Wj > (w+ - a(fr))/(1 + a(b~)).
where a(x) = [x(l - (a>+)2)]/[(l +.r)(w+ + x)]. It is straightforward to show that a(x) is increasing on the domain {ëã: x2 < ãî+). In particular, ct(b~) < a(w~) because b~ < w~ < w+ < 1, and therefore (b~)2, (èã)2 <
w+. Letting a = a(w~), we therefore obtain
Wj > (w+ - or)/(l + or),
which is the inequality claimed in the theorem.
It remains to dispose of the case j' = 1, that is, the maximin equilibrium has payoffs (1. b~) and w+ — b~. Change the tree T, by deleting the edge <?i- and adding the edge ej\. The result is a 1-tree Tj. Now
rfl = cij/icij + ÿ,) ë bj/(bj + &i) = aj/(cij + 1) ë bj/(bj + b~).
Since Wj = Uj ë bj and ÿ, < bj, it follows that
rji = Oj/(aj + 1) = Wj/(Wj + 1).
On the other hand, (A.23) implies that
rv > w+/(w+ + 1).
Putting these facts together, we obtain
rj. > W+/(W+ + 1) > Wj/(Wj + 1) = Tj\.
This implies that r(Ti) > r(Tj), which contradicts the assumption that r(Ty) < r(T) for all rooted trees T.
We now establish Pareto optimality. Suppose, by way of contradiction, that r(Tj) < r(T) for all rooted trees T, and there exists an equilibrium ê ô j that strictly dominates j:
cij < and bj < by. (A.26)
Let Tj be a j-tree having minimum reduced resistance among all rooted trees. If Tj contains an edge from ê to j, replace it by the oppositely directed edge ejk. By (A.20) and (A.26) r,k < Ãö, so this creates a /c-tree whose reduced resistance is less than that of Tj, which is a contradiction. Therefore ekj cannot be an edge in Tj.
Now consider any edge of form åù in Tj, where È ô ê. (There is at least one such edge if there is more than one coordination equilibrium.)
Replace åù with the edge ehk, and make a similar substitution for all edges that point toward j. In T, there is also a unique edge exiting from k, say, ew, where ê' ô j by the earlier part of the argument. Replace e^ with the edge e^. These substitutions yield a k-tree. We claim that it has strictly lower reduced resistance than T;. Indeed, (A.20) and (A.26) imply that for all Ii ô j, k, and all ê' ô j. k,
Ï,ê < rhj and rjk, < rue.
Hence all of the above substitutions result in a tree that has strictly lower reduced resistance. This contradiction shows that equilibrium j is not strictly Pareto dominated, and completes the proof of theorem 9.1.
NOTES
Chapter 1
1. For other evolutionary explanations of institutions based on game-theoretic concepts, see Schotter (1981), North (1986,1990), Sugden (1986), and Greif (1993).
2. See, e.g., Arthur, Ermoliev, and Kaniovski, 1984; and Arthur, 1989, 1994.
3. Roughly speaking, a Markov process is ergodicif the limiting proportion of time spent in each state exists and is the same for almost all realizations of the process.
4. See Menger, 1871,1883; Schotter, 1981; Marimon, McGrattan, and Sargent, 1990.
5. If the agent does not include his own previous choice in the calculation, the dynamic must be adjusted slightly near p' =.5.
6. See Katz and Shapiro, 1985; Arthur, 1989.
7. Moreover, there may be decreasing unit costs resulting from economies of scale and learning-by-doing effects, which would make an early lead all the more important.
8. This discussion is based on Hopper (1982), Hamer (1986), and Lay (1992), and on personal communications by Jean-Michel Goger and Arnulf Griibler for rules of the road in France and Austria.
9. This situation was first described by Rousseau (1762) and is known in the literature as the Stag Hunt Game.
10. In biology this represents a theory of evolution, whereas here we use the term simply to describe the look of a typical dynamic path.
11. See particularly Blume, 1993, 1995a; Brock and Durlauf, 1995; Anderlini and Ianni, 1996.
Chapter 2
1. We shall not enter the thicket of arguments as to whether dvorakactually is more efficient than qwerty,though there is no question that it was intendedto be more efficient (it was based on motion studies of typists' hand movements). For a detailed discussion of this issue see David (1985).
2. The replicator dynamic was first proposed in this form as a model of biological selection by Taylor and Jonker (1978).
3. For analytical treatments of this approach, see Weibull (1995), Binmore and Samuelson (1997), and Bjornerstedt and Weibull (1996).
4. See Bush and Mosteller, 1955; Suppes and Atkinson, 1960; Arthur, 1993; Roth and Erev, 1995; Borgers and Sarin, 1995,1996.
5. For variants of fictitious play and other belief updating processes, see Fu- denberg and Kreps, 1993; Fudenberg and Levine, 1993, 1998; Crawford, 1991, 1995; Kaniovski and Young, 1995; and Benai'm and Hirsch, 1996. For experimental data on learning see, e.g., van Huyck, Battalio, and Beil, 1990,1991; van Huyck, Battalio, and Rankin, 1995; Mookherjee and Sopher, 1994,1997; Cheung and Friedman, 1997; and Camerer and Ho, 1997.
6. See Schotter, 1981; Kalai and Jackson, 1997.
7. Miyasawa (1961) proved that under some tie-breaking rules, every fictitious play sequence in G must converge to a Nash equilibrium of G. Monderer and Shapley (1996a) showed that under anytie-breaking rule, every nondegenerate game has the fictitious play property. Monderer and Sela (1996) exhibit an example of a degenerate 2x2 game and a fictitious play process that fails to converge in the sense that no limit point is a Nash equilibrium of G.
8. B' is based on a particular tie-breaking rule. More generally, given any finite n-person game G, for each p e A,let B(p)be the set of all qˆ Ä such thatqi(Xj) >0 implies x, e BR,(p) for all iand all .v, á X,. The best-reply dynamic ispit) = B[P(t)} - pit)-This is a differential inclusion,that is, a set-valued differential equation. Since B(p)is upper semicontinuous, convex, and closed, the system has at least one solution from any initial point (Aubin and Cellina, 1984). For an analysis of the stability of Nash equilibrium in this process, see Hofbauer (1995).
9. Other games with the fictitious play property (under suitable tie-breaking rules) include dominance-solvable games (Milgrom and Roberts, 1990), games with strategic complementarities and diminishing returns (Krishna, 1992), and various Cournot oligopoly games (Deschamps, 1975; Thorlund-Petersen, 1990).
10. Monderer and Shapley, 1996b.
11.This idea can be substantially generalized, as we show in Chapter 7.
12. See Kami and Schmeidler (1990) for a discussion of fashion cycles. Jordan (1993) gives an example of a three-person game in which each person has two strategies and fictitious play cycles.
13. It is not essential that errors be made with uniform probability over different actions. See Chapter 5 for a discussion of this issue.
Chapter 3
1. This is known as the Picard-Lindelof theorem. For a proof, see Hirsch and Smale (1974), Chapter 8, or Hartman (1982, ch. 2).
2. This and other versions of monotonicity are discussed in Nachbar (1990), Friedman (1991), Samuelson and Zhang (1992), Weibull (1995), and Hofbauer and Weibull (1996).
3. A similar result holds under even weaker forms of monotonicity (Weibull, 1995, Proposition 5.11). In the multipopulation replicator dynamics defined in (3.6), strict Nash equilibria are in fact the onlyasymptotically stable states (Hofbauer and Sigmund, 1988; Ritzberger and Vogelsberger, 1990; Weibull, 1995). If G is a symmetric two-person game played by a single population of individuals, the replicator dynamic can have asymptotically stable states that are mixed Nash equilibria. Mixed evolutionarily stable strategies (ESSs) are an example. For a discussion of this case, see Hofbauer and Sigmund (1988) and Weibull (1995).
4. For this and other standard results on finite Markov chains, see Kemeny and Snell, 1960.
5. Theorem 3.1 is analogous to results of Freidlin and Wentzell (1984) on Wiener processes. Theorem 3.1 does not follow from their results, however, because they need various regularity conditions that we do not assume; furthermore, they only prove results for domains with no boundary. Analogous results for Wiener processes on bounded manifolds with reflecting boundary were obtained by Anderson and Orey (1976). The results of Anderson and Orey can be used to analyze the stochastic stability of Nash equilibria in a continuous framework, where the state space consists of the players' mixed strategies. This was the approach originally taken by Foster and Young (1990). In that paper we should have cited Anderson and Orey in addition to Freidlin and Wentzell for the construction of the potential function; this mistake was rectified in Foster and Young (1997).
The same conclusion holds even if everyone strict!]/prefers living in a mixed neighborhood to living in a homogeneous one. Suppose that each agent has utility h4 if one neighbor is like himself and one is different, utility i/° if both neighbors are like himself, and utility u~ if both neighbors are unlike himself, where u~< u°< ii*.Then the disadvantageous trades with least resistance (lowest net utility loss) are those in which either two people of the same type trade places, or else two people of the opposite type living in mixed neighborhoods trade places. All other disadvantageous trades have a larger net utility loss and therefore a greater resistance. As in the text, this suffices to show that the segregated states have strictly lower stochastic potential than the nonsegregated states.
Chapter 4
1. This terminology differs slightly from Harsanyi and Selten (1988), who use the term "risk dominance" to mean strictrisk dominance.
2. A strict Nash equilibrium is p-dominantif each action is the unique best reply to any belief that puts probability at least p on the other player playing his part of the equilibrium (Morris, Rob, and Shin, 1995).
3. A similar point is made by Binmore and Samuelson (1997).
Chapter 5
1. For discussions of urn schemes, see Eggenberger and Polya, 1923; Feller, 1950; Hill, Lane, and Sudderth, 1980; Arthur, Ermoliev, and Kaniovski, 1987.
2. The proof of theorem 5.1 is given in Kaniovski and Young (1995). Independently, Benaim and Hirsch (1996) proved a similar result. Arthur, Ermoliev, and Kaniovski (1987) pointed out that theorem 5.1 would follow from standard arguments in stochastic approximation if the process possessed a Lyapunov function, but they did not exhibit such a function. Fudenberg and Kreps (1993) used Lyapunov theory to treat the case of 2 x 2 games with a unique equilibrium (which is mixed) and stochastic perturbations arising from trembles in payoffs.
Chapter 6
1. For related work on local interaction models and their application, see Blume (1993, 1995a, 1995b), Ellison (1993), Brock and Durlauf (1995). Durlauf (1997), Glaeser, Sacerdote, and Scheinkman (1996), and Anderlini and lanni (1996).
2. Morris (1997) studies the amount of cohesiveness needed in an interaction network for a strategy to be able to propagate through the network purely by diffusion.
Chapter 7
1. Risk dominance is only one aspect of Harsanyi and Selten's theory of equilibrium selection. In example 7.2, however, the Harsanyi-Selten theory does select the risk dominant equilibrium, that is, the equilibrium that uniquely maximizes the product of the payoffs. As shown in the text, this is not the same as the stochastically stable equilibrium. In Chapter 8 we consider a particular class of coordination games known as Nash demand gamesin which the concepts of stochastic stability and risk dominance coincide.
2. In Hurkens's model, agents sample with replacement, that is, an agent can keep resampling a single previous action by another agent without realizing that he or she looked at it before. The model also assumes that an agent can have any belief about the probability of an action as long as the agent observed it at least once. (In our model, an agent's belief is determined by the frequency of each action in the agent's sample.) These substantially different assumptions imply that the process does not discriminate between minimal curb sets even when the sample size is large: every action that occurs in some minimum curb set occurs in some stochastically stable state (Hurkens, 1995). Sanchirico (1996) considers other classes of learning models that select minimal curb sets.
3. In the same spirit, Samuelson and Zhang (1992) show that if the continuous- time replicator dynamic starts in a strictly interior state, then it eliminates (iterated) strictly dominated strategies in the sense that the proportion of the population playing such strategies approaches zero over time.
Chapter 8
1. Given the assumption that a. b< 1/2, it can be shown (as in the proof of Theorem 4.1) that the discrete norms are the only recurrent classes of the process />'À"Ë'" when s = 0. When e > 0 and errors are local, the process is not necessarily irreducible. Nevertheless, it has a unique recurrent class, which is the same for all e > 0 and contains all the norms. The method described in the text for computing the stochastically stable norms via rooted trees remains valid in this case.
Date: 2016-04-22; view: 516