Theorem Triangle Inequality for Integration

Proof

Example Show that

Integration by Parts

Theorem Integration by Parts

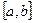Let and be two functions in . If and are continuous on , then

or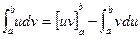

Example Show that (a) . (b)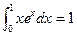

AL84II-1(a) For any non-negative integer k, let .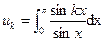

Express in terms of .

Hence, or otherwise, evaluate .

(b) For any non-negative integers and , let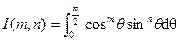

(i) Show that if 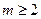, then

= .

(ii) Evaluate for .

(iii) Show that if , then

= .

(iv) Evaluate .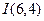

AL94II-11 For any non-negative integer , let

(a) (i) Show that .

[ Note: You may assume without proof that for . ]

(ii) Using (i), or otherwise, evaluate .

(iii) Show that for .

(b) For , let .

(i) Using (a)(iii), or otherwise, express in terms of .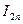

(ii) Evaluate .

Example . ( ans: )

Solution Let

Example Show that (a)

(b)

Deduce that

Continuity and Differentiability of a Definite Integral

Theorem Mean Value Theorem for Integral

If is continuous on [a,b] then there exists some c in [a,b] and

Proof

Theorem Continuity of definite Integral

If is continuous on 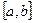and let 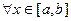then is continuous at each point x in .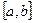

Proof

Theorem * Fundamental Theorem of Calculus

Let be continuous on [a,b] and 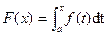. Then ,

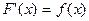Proof

Remark :

Proof

Example Evaluate the Derivatives of the following

(i)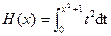

(ii)

(iii)

Solution

ExampleLet be a function which is twice-differentiable and with continuous second derivative. Show that , .

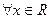Example Let .

Prove that .

AL90II-5(a) Evaluate , where is continuous and is a positive integer.

(b) If , find

ExampleEvaluate

AL97II-5(b) Evaluate .

AL98II-2 Let be a continuous periodic function with period .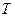

(a) Evaluate

(b) Using (a), or otherwise, show that for all .

ExampleLet be a positive integer.

Evaluate (a)

(b)

(c)

Example Suppose has a continuous derivative on [0,1]. If for all and

find .

Remark 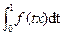is a function of and so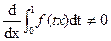

Improper Integrals

Definition A definite integral is called improper integral if the interval [a,b] of integration is infinite, or if is not defined or not bounded at one or more points in [a,b].

Example , , , are improper integral.

Definition (a) is defined as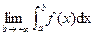

(b) is defined as

(c) 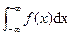is defined as for any real number .

( Or )

(d) If is continuous except at a finite number of points, say where

, then is defined to be

for any 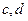such that .

Definition The improper integral is said to be Convergent or Divergent according to the improper integral exists or not.

Example Evaluate (a) (b)

Example Evaluate

Example Evaluate

Theorem Let and be two real-valued function continuous for . If then the fact that 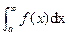diverges implies diverges and the fact that

converges implies that 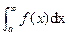converges.

Example Discuss whether is convergence?

Example For any non-negative integer , define

.

(a) Show if is positive integers, then .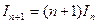

Hence, if is convergent, is also convergent.

(b) Find .

Date: 2016-04-22; view: 1044