Theorem Cauchy-Inequality for Integration

Definite Integrals

Definition Let be a continuous function defined on 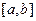divide the interval by the points

from to into subintervals. (not necessarily equal width) such that when 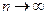, the length of each subinterval will tend to zero.

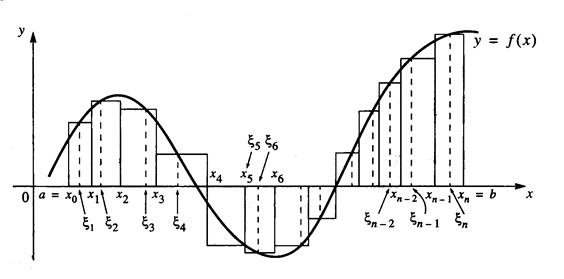
In the i^th subinterval choose for . If exists and is independent of the particular choice of and , then we have

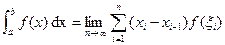
Remark For equal width, i.e. divide into equal subintervals of length, i.e. ,

we have .

Choose and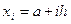

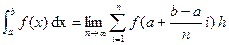
OR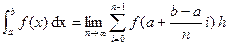

Example Evaluate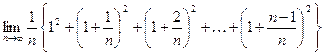

Example =

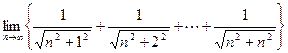
Example Using a definite integral, evaluate

(a)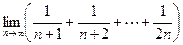

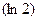
(b)

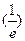
AL95II(a) Evaluate , where .

(b) By considering a suitable definite integral, evaluate

AL83II-1 Evaluate (a) ,

(b) , [ Hint: Put .]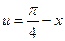

(c)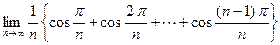

Example* =

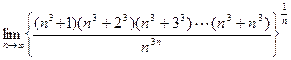
Properties of Definite Integrals

P1 The value of the definite integral of a given function is a real number, depending on its lower

and upper limits only, and is independent of the choice of the variable of integration, i.e.

.

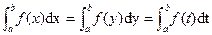P2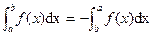

P3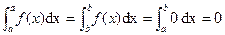

P4 Let , then

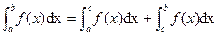
Example (a) (b) (c)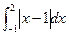

P5* Comparison of two integrals

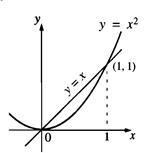If , then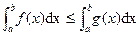

Example , for all ;

hence .

Example Prove that (a) .

(b)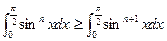

ExampleIn Figure, is tangent to the curve at , where .

By considering the area of 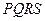, show that

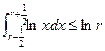
Hence show that for any integer .

P6 Rules of Integration

If are continuous function on then

(a) for some constant k.

(b) .

P7* (a) 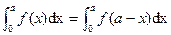. a : any real constant.

(b) .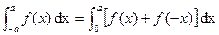

(c)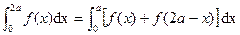

(d)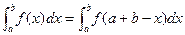

Proof(a)

Example Evaluate (a) (b)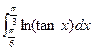

Exercise 7C

5. By proving that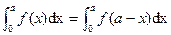

evaluate (a) (b)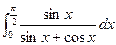

6 (a) Show that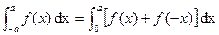

(b) Using (a), or otherwise, evaluate the following integrals:

(i) (iii)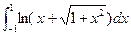

Remind are odd functions.

are even functions.

Graph of an odd functionGraph of an even function

P8 (i) If (Even Function)

then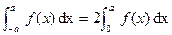

(ii) If (Odd Function)

then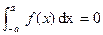

Proof

ExampleEvaluate (a) (b)

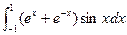
Example Prove that (a) (b)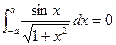

Definition Let be a subset of , and be a real-valued function defined on . is called a periodic function if and only if there is a positive real number T such that 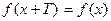, for 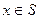. The number T is called the period.

P9 If is periodic function, with period 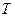i.e.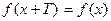

(a)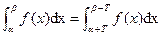

(b)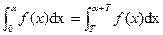

(c)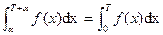

(d) for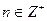

Proof

Theorem Cauchy-Inequality for Integration

If , are continuous function on 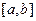, then

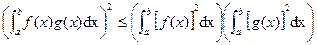
Proof

Example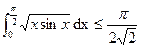

Date: 2016-04-22; view: 1060