
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Measures of Dispersion
In statistics, dispersion (also called variation) shows how your data is distributed (or spread out). Common measures are range and standard deviation.



To calculate the SD:
1. Find the mean of the distribution.
2. Subtract each score from the mean.
3. Square each result (deviation).
4. Add the squared deviations together.
5. Divide by the total number of scores (n-1) you subtract 1 to get rid of any outliers.
6. This result is called the variance.
7. Find the square root of the variance. This is the SD.
8. Now you can compare the mean to the SD.
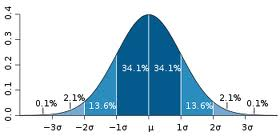
Ex: compare 3 class scores out of 100: 78, 80, 92; 2/3 of your scores are 1 SD from the mean.
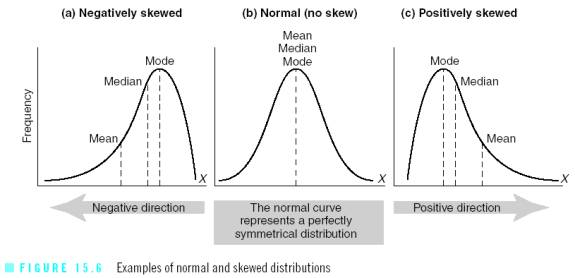
Skewed Data
Once you have drawn your range or standard deviation, you may notice that your data is skewed right or left (positive or negative). A normal range of distribution is double-tailed (2 tailed) as in the example of a SD on the previous page. A skew usually indicates that the data is single-tailed (left or right).
Your wording of your hypothesis may also determine your tail (example: changing temperature in the room will increase the time needed to complete the math test).
· A negative skew means that the tail is on the left side. The bulk of responses are to the right of the mean.
· A positive skew means that the tail is on the right side. The bulk of responses are to the left of the mean.
This is usually because of outliers in your data:
· 1 participant is much older than the average.
· 1 participant is much better (or worse) at the task (DV).
· 1 participant has an extremely high (or low) IQ.
| Scoring E. Results: Descriptive: (2 marks) q Results are clearly stated. q Results accurately reflect the hypothesis of the research. q Appropriate descriptive statistics (one measure of central tendency and one measure of dispersion) are applied to the data and their use is explained. q The graph of results is accurate, clear, and directly relevant to the hypothesis of the study. q Results are presented in both words and tabular form. |
· Vertical (y-axis, DV)
· Horizontal (x-axis, IV)
Bar-graphs are good to compare categories. Histograms are good for a continuous IV.
 F. Results: Inferential Statistics
F. Results: Inferential Statistics
Even if you suffer from calculatophobia (fear of statistics), you must include inferential statistical analysis of your results in this section.
You probably have some idea of the results that you wanted from your experiment. Do not try to be a cheerleader rooting for your specific results. In research, you want to be a non-partisan (not taking sides) bystander. Don’t be so in love with your outcome that you lose your professional objectivity and become biased in your evaluation of the data. You must interpret the data regardless of the outcome—even if you failed to show a significant change between rock music and classical music (for example).
Inferential statistics ask if your random sample really represents the whole population. Can we infer from the small group how the large group would behave?
· Example: Could I ask 10% of the class to place a vote on something, and then apply that vote to the entire class?
· Could 1 handful of beans tell me the health and taste of the entire bin of beans?
· If 10 states voted for one presidential candidate, could we infer that the rest of the country will likely vote the same way?
· Is it likely that the math anxiety experienced by economics majors could be applied to the entire population of people majoring in economics that could have been sampled?
The Null Hypothesis (N0)
The Null Hypothesis (N0) assumes that there is no significant difference in your data. In statistics, The Null is assumed to be true…your experiment is either proving the Null to be right or wrong. Think of this like a court of law where you are assumed innocent until proven guilty.
So, if the starting assumption is the NULL hypothesis (N0), than this means the results of your experiment were caused by probability or chance (like flipping a coin). This also means that your IV (Independent Variable) did not really have an effect. To test this theory, we need to conduct an inferential statistics test.
For example: I flip a coin 20 times while listening to heavy metal rock music. My results are 11 heads and 9 tails. A statistical test would show no real effect from the rock music. The results were probably just chance.
The further apart your observed results are from your expected results, the more likely it is that your IV (rock music) really did make a difference (example: if my results were 3 tails to 17 heads).
Do I Accept or Reject the Null Hypothesis?
The goal of research is to either accept or reject the null hypothesis. We want to establish that there actually is a relationship between the IV and DV and that any results we have obtained were not just due to chance.
Again, working off of your null hypothesis, if the null is true…then there is no significant difference caused by your Independent Variable (IV). This means you could have played rock music, classical music, or no music and the results would have been the same.
· This statistics test will establish that the results are not due to chance.
· This means that the data are significant (95% or higher, or p<0.05).
· When the data are significant (95% or higher, or p<0.05) we ”reject the null hypothesis.” This simply means that the IV did cause significant changes in the DV.
· When our hypothesis is not proven to be statistically significant, we must ”accept the null hypothesis.” (You can score just as high in the IA process even if you have to accept the null. The fact that you understand why and how is what is important).
After analyzing your data with inferential statistics, you need to make a decision on the significance of your findings. Were your results due to a real difference between the groups, or were they the result of chance or error?
Here are some examples of how to properly state the null:
· “The results were found to be significant (p<0.05), which means that the probability of the results occurring by chance if the null hypothesis were true is less than 5%. Therefore the null hypothesis was rejected and the research hypothesis was accepted. There does appear to be a real difference in the number of words recalled by males and females.”
· “A chi-squared (X2) test was carried out because the data were nominal and two independent samples were being compared. A significant difference was found (X2=4.78, p<0.05) and we can therefore reject the null hypothesis.”
· “There was a significant difference between the number of letters recalled by the experimental group and the control group. (X2=4.2, (degree of freedom) d.f.=1, p<0.05)”
Finding the Best Statistical Test
There are 3 statistical tests that are generally used for the IA:
· Chi-Squared Test
· Mann-Whitney U Test
· Wilcoxon Signed-Ranks Test
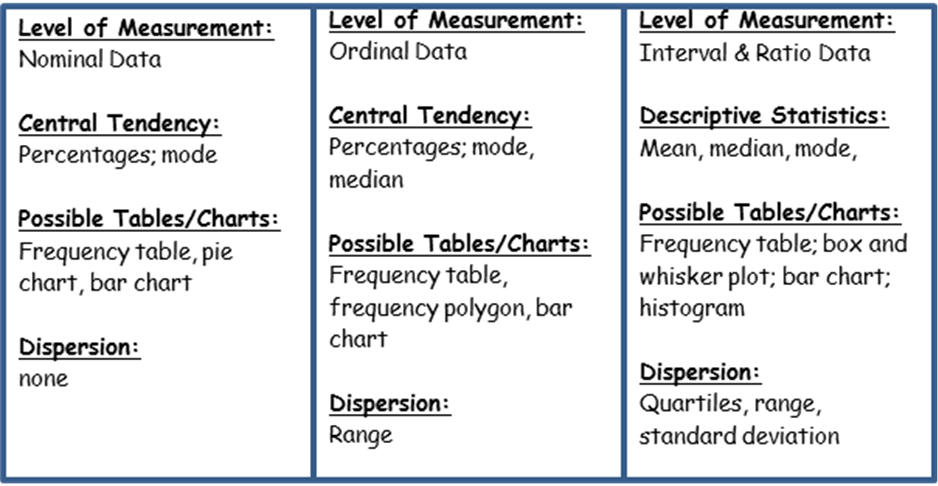
You should refer to the design of your experiment and the level of measurement of your data to justify your choice. You will need to explain why you chose the test that you did. The charts below should help you make a solid decision in selecting the right test for the job.
· Parametric: if the data is ratio or interval, evenly distributed (homogenous, bell curve), often best with a large sample. A T-Test is an example (not a recommended choice).
· Nonparametric: if the data is ordinal or nominal, this test gets rid of outliers if your data is skewed (important because of our small sample size).
Next, figure out if you need a paired or unpaired test (also based on the design method used).
· Paired: when you use the same people (repeated measures), the values are matched (before & after with the same group).
· Unpaired: when you use 2 groups of people (independent sample), when the values are not matched (control & experimental group, smokers & non-smokers).

Chi-Squared Test: used for nominal data in an independent samples design in an experiment testing the difference between two conditions (or categories).
· Examples: dog people or cat people; smokers & non-smokers; wear glasses & don’t wear glasses; Republicans & Democrats; male & female.
Mann Whitney U Test: used for ordinal data (or higher data) in an independent samples design in an experiment testing the difference between two conditions.
· Examples: The control group solved a puzzle with no noise, the experimental group solved the puzzle with loud music playing.
· The control group performed a task alone, the experimental group performed a task in front of others (social facilitation).
· The control group memorized a word list. The experimental group smelled vanilla while memorizing a word list.
Wilcoxon Signed Ranks Test: used for at least ordinal data (or higher data) in a repeated measures design in an experiment testing the difference between two conditions.
· Examples: Before and after; same group of 10 participants.
· A group of 10 first tried to learn new words; then the same group tried to learn new words with pictures next to them.
· A group of 10 first tried to solve a puzzle with no noise; then the same group tried to solve a puzzle with white noise playing in their ears.
For video explanations of these tests, visit: www.statisticslectures.com
You can double check your calculations at: www.graphpad.com/quickcalcs/index.cfm
The Chi-Squared (X2) Test
When you are interested in the relationship between 2 categories, you can use a chi-squared test.
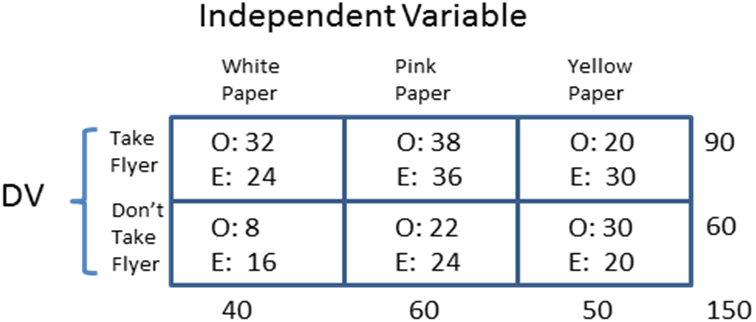
Example: Students created flyers on different kinds of color paper—white paper, pink paper, and yellow paper. They watch the table to see if participants would take a white flyer, a pink flyer, or a yellow flyer.
STEP 1: Draw a chart with boxes.

STEP 2: Fill in the boxes with the results that you observed (O=observed results).
STEP 3: Add up the observed numbers to be sure your math is correct (columns and rows).

STEP 4: Find the expected results (E) for each cell. Take the column total X the row total then divide by the total number of participants. Columns go up and down; rows go across.
Example: 90 x 40 / 150 = 24

· O: Observed: the data that actually happened.
· E: Expected: The expected amount that there should be (based on percentages).
· The further apart the observed is from the expected, the more likely that there is a significant difference.
STEP 5: Double check that the expected values also add up to the column and row total.
STEP 6: (Almost Done!) Now you have to plug each cell into the formula.

· Cell 1: (O-E)2 divided by E = (32-24)2/24= (8)2/24 = 64/24 = 2.6
· Cell 2: (O-E)2 divided by E = (38-36)2/36 = (2)2/36 = 4/36 = 0.11
· Cell 3: (O-E)2 divided by E = (20-30)2/30 = (-10)2/30 = 100/30 = 3.33
· Cell 4: (O-E)2 divided by E = (8-16)2/16 = (-8)2/16 = 64/16 = 4
· Cell 5: (O-E)2 divided by E = (22-24)2/24 = (-2)2/24 = 4/24 = 0.166
· Cell 6: (O-E)2 divided by E = (30-20)2/20 = (10)2/20 = 100/20 = 5
STEP 7: Add the total number of cells. Total: 15.206
STEP 8: Now you check a Chi-Squared Chart/Table to see if your results show significance.
· For Chi-Squared tests, there is a number called the “degrees of freedom” (df) which has to do with how many columns and rows you used. To calculate the df you use the following formula: the # of rows in your table-1; multiply that by the number of columns -1= df.
Here is the easy version:
1 df (4 cells) your answer must be greater than (>) 3.84 in order to be significant (p<0.05). Anything less than (<) 3.84 means you must accept the NULL.
2 df (6 cells) must be greater than (>) 5.99. Anything less means you must accept the NULL.
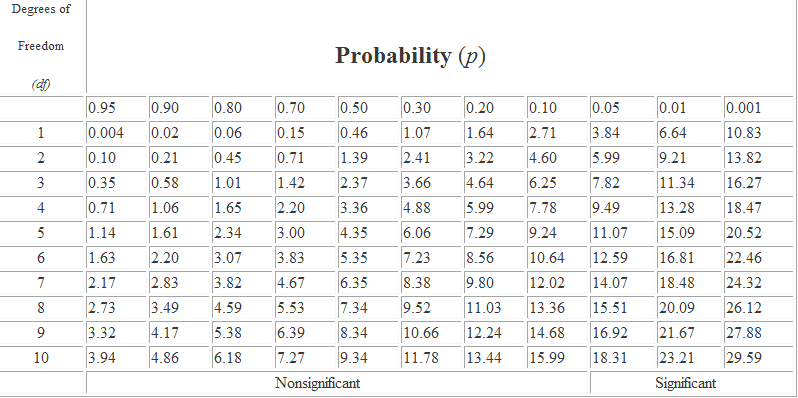
Chi-Square Chart
Mann-Whitney U
(also called the Mann–Whitney–Wilcoxon (MWW) or Wilcoxon rank-sum test)
STEP 1: Rank all of your scores in order from lowest (Rank 1) to highest (Rank 15). Do this together for both groups—Control Group and Experimental Group.
*My example only goes to 15, but if you used 20 participants, then Rank all the way to 20.
Rank: 1, 2, 3, 4, 5, 6, 7, 8, 9. . .20
STEP 2: Add the sum of each group.
Date: 2015-01-11; view: 4964
| <== previous page | | | next page ==> |
| Control Group Experimental Group | | | Experimental Group Control Group |