
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Other Sources of Reflections
Much of what has been said about ground reflections applies to reflections from other objects as well. The "ground reflection" on a particular path may be from a building rooftop rather than the ground itself, but the effect is much the same. On long links, reflections from objects near the line of the direct path will almost always cause increased path loss - in essence, you have a permanent "flat fade" over a very wide bandwidth. Reflections from objects which are well off to the side of the direct path are a different story, however. This is a frequent occurrence in urban areas, where the sides of buildings can cause strong reflections. In such cases, the angle of incidence may be much larger than zero, unlike the ground reflection case. This means that horizontal and vertical polarization may behave quite differently - as we saw in Fig. 8, vertically polarized signals tend to produce lower-amplitude reflections than horizontally polarized signals when the angle of incidence exceeds a few degrees. When the reflecting surface is vertical, like the side of a building, a signal which is transmitted with horizontal polarization effectively has vertical polarization as far as the reflection is concerned. Therefore, horizontal polarization will generally result in weaker reflections and less multipath than vertical polarization in these cases.
Effects of Rain, Snow and Fog
The loss of LOS paths may sometimes be affected by weather conditions (other than the refraction effects which have already been mentioned). Rain and fog (clouds) become a significant source of attenuation only when we get well into the microwave region. Attenuation from fog only becomes noticeable (i.e., attenuation of the order of 1 dB or more) above about 30 GHz. Snow is in this category as well. Rain attenuation becomes significant at around 10 GHz, where a heavy rainfall may cause additional path loss of the order of 1 dB/km.
Path Loss on Non-Line of Sight Paths
We have spent quite a bit of time looking at LOS paths, and described the mechanisms which often cause them to have path loss which differs from the "free space" assumption. We've seen that the path loss isn't always easy to predict. When we have a path which is not LOS, it becomes even more difficult to predict how well signals will propagate over it. Unfortunately, non-LOS situations are sometimes unavoidable, particularly in urban areas. The following sections deal with some of the major factors which must be considered.
Diffraction Losses
In some special cases, such as diffraction over a single obstacle which can be modeled as a knife edge, the loss of a non-LOS path can be predicted fairly readily. In fact, this is the same situation that we saw in Figures 1 and 2, with the diffraction parameter  > 0. This parameter, from equation (8), is
> 0. This parameter, from equation (8), is

To get  d, measure the straight-line distance between the endpoints of the link. Then measure the length of the actual path, which includes the two endpoints and the tip of the knife edge, and take the difference between the two. The geometry is shown in Fig. 7(a), the "positive h" case. A good approximation to the knife-edge diffraction loss in dB can then be calculated from
d, measure the straight-line distance between the endpoints of the link. Then measure the length of the actual path, which includes the two endpoints and the tip of the knife edge, and take the difference between the two. The geometry is shown in Fig. 7(a), the "positive h" case. A good approximation to the knife-edge diffraction loss in dB can then be calculated from
 (12)
(12)
Example 3. We want to run a 915 MHz link between two points which are a straight-line distance of 25 km apart. However, 5 km from one end of the link, there is a ridge which is 100 meters higher than the two endpoints. Assuming that the ridge can be modeled as a knife edge, and that the paths from the endpoints to the top of ridge are LOS with adequate Fresnel zone clearance, what is the expected path loss? From simple geometry, we find that length of the path over the ridge is 25,001.25 meters, so that d = 1.25 m. Since  = 0.33 m, the parameter
= 0.33 m, the parameter  , from (8), is 3.89. Substituting this into (12), we find that the expected diffraction loss is 24.9 dB. The free space path loss for a 25 km path at 915 MHz is, from equation (6a), 119.6 dB, so the total predicted path loss for this path is 144.5 dB. This is too lossy a path for many WLAN devices. For example, suppose we are using WaveLAN cards with 13 dBi gain antennas, which (disregarding feed line losses) brings them up to the maximum allowable EIRP of +36 dBm. This will produce, at the antenna terminals at the other end of the link, a received power of (36 - 144.5 + 13) = -95.5 dBm. This falls well short of the -78 dBm requirement of the WaveLAN cards. On the other hand, a lower-speed system may be quite usable over this path. For instance, the FreeWave 115 Kbps modems require only about -108 dBm for reliable operation, which is a comfortable margin below our predicted signal levels.
, from (8), is 3.89. Substituting this into (12), we find that the expected diffraction loss is 24.9 dB. The free space path loss for a 25 km path at 915 MHz is, from equation (6a), 119.6 dB, so the total predicted path loss for this path is 144.5 dB. This is too lossy a path for many WLAN devices. For example, suppose we are using WaveLAN cards with 13 dBi gain antennas, which (disregarding feed line losses) brings them up to the maximum allowable EIRP of +36 dBm. This will produce, at the antenna terminals at the other end of the link, a received power of (36 - 144.5 + 13) = -95.5 dBm. This falls well short of the -78 dBm requirement of the WaveLAN cards. On the other hand, a lower-speed system may be quite usable over this path. For instance, the FreeWave 115 Kbps modems require only about -108 dBm for reliable operation, which is a comfortable margin below our predicted signal levels.
To see the effect of operating frequency on diffraction losses, we can repeat the calculation, this time using 144 MHz, and find the predicted diffraction loss to be 17.5 dB, or 7.4 dB less than at 915 MHz. At 2.4 GHz, the predicted loss is 29.0 dB, an increase of 4.1 dB over the 915 MHz case (these differences are for the diffraction losses only, not the only total path loss).

Figure 9 Diffraction by a Rounded Obstacle
Unfortunately, the paths which digital experimenters are faced with are seldom this simple. They will frequently involve diffraction over multiple rooftops or other obstacles, many of which don't resemble knife edges. The path losses will generally be substantially greater in these cases than predicted by the single knife edge model. The paths will also often pass through objects such as trees and wood-frame buildings which are semi-transparent at radio frequencies. Many models have been developed to try and predict path losses in these more complex cases. The most successful are those which deal with restricted scenarios rather than trying to cover all of the possibilities. One common scenario is diffraction over a single obstacle which is too rounded to be considered a knife edge. There are different ways of treating this problem; the one described here is from Ref. [3]. The top of the object is modeled as a cylinder of radius r, as shown in Fig. 9. To calculate the loss, you need to plot the profile of the actual object, and then draw straight lines from the link endpoints such that they just graze the highest part of the object as seen from their individual perspectives. Then the parameters Ds, d1, d2 and are estimated, and an estimate of the radius r can then be calculated from
 (13)
(13)
Note that the angle is measured in radians. The procedure then is to calculate the knife edge diffraction loss for this path as outlined above, and then add to it an excess loss factor Lex, calculated from
 (14)
(14)
There is also a correction factor for roughness: if the object is, for example, a hill which is tree-covered rather than smooth at the top, the excess diffraction loss is said to be about 65% of that predicted in (14). In general, smoother objects produce greater diffraction losses.
Example 4. We revisit the scenario in Example 3, but let's suppose that we've now decided that the ridge blocking our path doesn't cut it as a knife edge (ouch!). From a plot of the profile, we estimate that Ds = 10 meters. As before, d1 = 20 km, d2 = 5 km and the height of the ridge is 100 meters. Dusting off our high school trigonometry, we can work out that  = 1.43, or 0.025 radians. Now, plugging these numbers into (13), we get r = 188 meters. Then, with
= 1.43, or 0.025 radians. Now, plugging these numbers into (13), we get r = 188 meters. Then, with  = 0.33 m, we can calculate the excess loss from (14):
= 0.33 m, we can calculate the excess loss from (14):
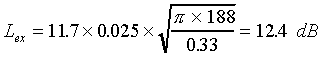
So, summed with the knife edge loss calculated previously, we have an estimated total diffraction loss of 37.3 dB (assuming the ridge is "smooth" rather than "rough"). This is a lot, but you can easily imagine scenarios where the losses are much greater: just look at the direct dependence on the angle in (14) and picture from Fig. 9 what happens when the obstacle is closer to one of the link endpoints. Amateurs doing weak signal work are accustomed to dealing with large path losses in non-LOS propagation, but such losses are usually intolerable in high-speed digital links.
Date: 2016-03-03; view: 1008
| <== previous page | | | next page ==> |
| Diffraction and Fresnel Zones | | | Attenuation from Trees and Forests |