Module № 5. Questions.

1. Mechanisms of mass transfer. Examples of mass transfer processes.

Mass transfer is the movement of a chemical species in a mixture or solution usually due to presents of a concentration gradient of the species. Mass transfer may occur in liquid or a solid solution.

In other words, mass transfer is the net movement of mass from one location, usually meaning a stream, phase, fraction or component, to another. Mass transfer occurs in many processes, such as absorption, evaporation, adsorption, drying, precipitation, membrane filtration, and distillation. Mass transfer is used by different scientific disciplines for different processes and mechanisms. The phrase is commonly used in engineering for physical processes that involve diffusive and convective transport of chemical species within physical systems.

Some common examples of mass transfer processes are the evaporation of water from a pond to the atmosphere, the purification of blood in the kidneys and liver, and the distillation of alcohol. In industrial processes, mass transfer operations include separation of chemical components in distillation columns, absorbers such as scrubbers, adsorbers such as activated carbon beds, and liquid-liquid extraction.

2. Difference between heat and mass transfer processes.

Heat transfer deals with the movement of heat and temperature gradients. The three types of heat transfer are conduction, convection, and radiation. Mass transfer deals with concentrations of a particular substance. Types of mass transfer include diffusion and convection.

Heat transfer and mass transfer are kinetic processes that may occur and be studied separately or jointly.

Studying them apart is simpler, but both processes are modelled by similar mathematical equations in the

case of diffusion and convection (there is no mass-transfer similarity to heat radiation), and it is thus more

efficient to consider them jointly. Besides, heat and mass transfer must be jointly considered in some cases like evaporative cooling and ablation.

The usual way to make the best of both approaches is to first consider heat transfer without mass transfer,

and present at a later stage a briefing of similarities and differences between heat transfer and mass

transfer, with some specific examples of mass transfer applications. Following that procedure, we forget

for the moment about mass transfer (dealt with separately under Mass Transfer), and concentrate on the

simpler problem of heat transfer.

There are complex problems where heat and mass transfer processes are combined with chemical

reactions, as in combustion; but many times the chemical process is so fast or so slow that it can be

decoupled and considered apart, as in the important diffusion-controlled combustion problems of gas-fuel

jets, and condensed fuels (drops and particles), which are covered under Combustion kinetics. Little is

mentioned here about heat transfer in the micrometric range and below, or about biomedical heat transfer

(see Human thermal comfort).

The analogy between Convective Heat and Mass transfer

Conduction and diffusion in a fluid are governed by physical laws of identical

mathematical form,that is, Fourier's and Fick's laws respectively. And in most gas

mixtures Sherwood and Stanton numbers are nearly equal to their heat transfer

counterparts. For dilute mixtures and solutions and low mass transfer rates the

analogy is simple. For the same flow conditions the Sherwood or Stanton Number

,s obtained by replacing the Prandtl Number by the Schmidt Number in

appropriate heat transfer correl ation.

For example, in the case of fully developed flow in a smooth pipe:

Nua: 0.023 Redos Prol; Pr>0.5

Nt'ta: 0'023 Redo'8 S"o,; Sc>,'

3. Expressions of mass species concentrations.

The terms mass convection or convective mass transfer are generally used to

describe the process of mass transfer between a surface and moving fluid. The

surface may be that of falling water film in air humidifier, of a coke particle in a

gasifier. As was the case for heat convection, the flow may be forced or natural,

internal and external, and laminar or turbulent. In addition, the concept of whether

the mass transfer rate is low or high place an important role: when mass transfer

rate are low, there is a simple analogy between heat transfer and mass transfer that

can be efficiently exploited in the solution of engineering problems.

Analogous to convective heat transfer, the rate of mass transfer by convection

is usually a complicated function of surface geometry and s-surface composition,

the fluid composition and velocity, and fluid physical properties.

For simplicity, we will restrict our attention to fluids that are either binary

mixtures or solutions. Referring to fig. 1 we define the mass transfer conductance

of species l, gm1, by relation:

j 1,s=g∆m1; (1)

∆m1=m1,s-m1,e

where j 1,s- is diffusive mass flux of species 1 (kg/m2s);

tnt 1 is mass fraction of species 1.

Fig. 1

The units of gm1 are seen to be the same as for mass flux (kg/m2 s).

Equation (1) is a similar form to Newton's law, which defined the heat transfer

coefficient α.

On molar basis, we define the mole transfer conductance of species 1, Gm1, by a

coffesponding relation,

J1,s= Gm1 ∆x1; (2)

∆X1 = X1,s – X1,e,

where J1,s--is diffusive molar flux of species 1 (kmol/m2 s);

1 Notation for convective

x 1 - is mole fraction of species 1 .

4. Mass diffusion. Physical mechanisms of mass diffusion.

5. The first Fick’s law. Diffusion coefficient.

5.Fick's first law relates the diffusive flux to the concentration under the assumption of steady state. It postulates that the flux goes from regions of high concentration to regions of low concentration, with a magnitude that is proportional to the concentration gradient (spatial derivative). In one (spatial) dimension, the law is

where

• is the "diffusion flux" [(amount of substance) per unit area per unit time], example . measures the amount of substance that will flow through a small area during a small time interval.

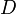• is the diffusion coefficient or diffusivity in dimensions of [length² time⁻¹], example

• (for ideal mixtures) is the concentration in dimensions of [amount of substance per unit volume], example

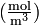
• is the position [length], example

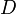is proportional to the squared velocity of the diffusing particles, which depends on the temperature, viscosity of the fluid and the size of the particles according to the Stokes-Einstein relation. In dilute aqueous solutions the diffusion coefficients of most ions are similar and have values that at room temperature are in the range of 0.6x10⁻⁹ to 2x10⁻⁹ m²/s. For biological molecules the diffusion coefficients normally range from 10⁻¹¹ to 10⁻¹⁰ m²/s.

In two or more dimensions we must use , the del or gradient operator, which generalises the first derivative, obtaining

.

The driving force for the one-dimensional diffusion is the quantity

which for ideal mixtures is the concentration gradient. In chemical systems other than ideal solutions or mixtures, the driving force for diffusion of each species is the gradient of chemical potential of this species. Then Fick's first law (one-dimensional case) can be written as:

where the index i denotes the ith species, c is the concentration (mol/m³), R is the universal gas constant (J/(K mol)), T is the absolute temperature (K), and μ is the chemical potential (J/mol).

If the primary variable is mass fraction ( , given, for example, in ), then the equation changes to:

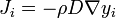
where is the fluid density (for example, in ). Note that the density is outside the gradient operator.

6. Steady diffusion through a plane wall. Diffusion resistance.

7. Transient diffusion. The second Fick’s law.

Fick's second law

Fick's second law predicts how diffusion causes the concentration to change with time:

where

· is the concentration in dimensions of [(amount of substance) length⁻³], example

· is time [s]

· is the diffusion coefficient in dimensions of [length² time⁻¹], example

· is the position [length], example

It can be derived from Fick's First law and the mass conservation in absence of any chemical reactions:

Assuming the diffusion coefficient D to be a constant we can exchange the orders of the differentiation and multiply by the constant:

and, thus, receive the form of the Fick's equations as was stated above.

For the case of diffusion in two or more dimensions Fick's Second Law becomes

,

which is analogous to the heat equation.

If the diffusion coefficient is not a constant, but depends upon the coordinate and/or concentration, Fick's Second Law yields

An important example is the case where is at a steady state, i.e. the concentration does not change by time, so that the left part of the above equation is identically zero. In one dimension with constant , the solution for the concentration will be a linear change of concentrations along . In two or more dimensions we obtain

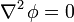
which is Laplace's equation, the solutions to which are called harmonic functions by mathematicians.

8. Mass convection. Dimensionless groups and dimensionless equations for mass convection.

The convection zone of a star is the range of radii in which energy is transported primarily by convection. In the radiation zone, energy is transported by radiation. Stellar convection consists of mass movement of plasma within the star which usually forms a circular convection current with the heated plasma ascending and the cooled plasma descending.

The Schwarzschild criterion expresses the conditions under which a region of a star is unstable to convection. A parcel of gas that rises slightly will find itself in an environment of lower pressure than the one it came from. As a result, the parcel will expand and cool. If the rising parcel cools to a lower temperature than its new surroundings, so that it has a higher density than the surrounding gas, then its lack of buoyancy will cause it to sink back to where it came from. However, if the temperature gradient is steep enough (i. e. the temperature changes rapidly with distance from the center of the star), or if the gas has a very high heat capacity (i. e. its temperature changes relatively slowly as it expands) then the rising parcel of gas will remain warmer and less dense than its new surroundings even after expanding and cooling. Its buoyancy will then cause it to continue to rise. The region of the star in which this happens is the convection zone.

In stars more than 1.3 times the mass of the Sun, the nuclear fusion of hydrogen into helium occurs via CNO cycle instead of the proton-proton chain. The CNO process is very temperature sensitive, so the core is very hot but the temperature falls off rapidly. Therefore, the core region forms a convection zone that uniformly mixes the hydrogen fuel with the helium product. The core convection zone of these stars is overlaid by a radiation zone that is in thermal equilibrium and undergoes little or no mixing.[1]

In stars of less than about 10 solar masses, the outer envelope of the star contains a region where partial ionization of hydrogen and helium raises the heat capacity. The relatively low temperature in this region simultaneously causes the opacity due to heavier elements to be high enough to produce a steep temperature gradient. This combination of circumstances produces an outer convection zone, the top of which is visible in the sun as solar granulation. Low mass main sequences of stars, such as red dwarfs below 0.35 solar masses,[2] as well as pre-main sequence stars on the Hayashi track, are convective throughout and do not contain a radiation zone.

9. The analogy between heat and mass convection.

The analogy between Convective Heat and Mass transfer

Conduction and diffusion in a fluid are governed by physical laws of identical

mathematical form,that is, Fourier's and Fick's laws respectively. And in most gas

mixtures Sherwood and Stanton numbers are nearly equal to their heat transfer

counterparts. For dilute mixtures and solutions and low mass transfer rates the

analogy is simple. For the same flow conditions the Sherwood or Stanton Number

,s obtained by replacing the Prandtl Number by the Schmidt Number in

appropriate heat transfer correl ation.

For example, in the case of fully developed flow in a smooth pipe:

Nua: 0.023 Redos Prol; Pr>0.5

Nt'ta: 0'023 Redo'8 S"o,; Sc>,'

10. Air-fuel mixtures. Stoichiometric composition of air-fuel mixture.

11. The first law of thermodynamics for chemical reactions.

12. Reaction heat at constant pressure and constant volume. Combustion heat.

Enthalpy (H) is the sum of the internal energy (U) and the product of pressure and volume (PV) given by the equation:

H = U + PV

When a process occurs at constant pressure, the heat evolved (either released or absorbed) is equal to the change in enthalpy. Enthalpy is a state function which depends entirely on the state functions T, P and U. Enthalpy is usually expressed as the change in enthalpy (ΔH) for a process between initial and final states:

ΔH = ΔU + ΔPV

Also at constant pressure the heat flow(q) for the process is equal to the change in enthalpy defined by the eqation:

ΔH = q

By looking at whether q is exothermic or endothermic we can determine a relationship between ΔH and q. If the reaction absorbs heat it is endothermic meaning the reaction consumes heat from the surroundings so q > 0 (positive). Therefore, at constant temperature and pressure, by the equation above, if q is positive then ΔH is also positive. And the same goes for if the reaction releases heat, then it is exothermic, meaning the system gives off heat to its surroundings, so q < 0 (negative). And if q is negative then ΔH will also be negative.

Heats of Reaction and Enthalpy Change ΔH—For any reaction occurring at constant temperature, the heat of reaction is the quantity of heat exchanged between the reaction system and its surroundings. If a reaction is carried out at constant volume, the heat of reaction at constant volume (qv) is equal to the change in internal energy (ΔU). For constant-pressure processes, enthalpy (H) is a more useful property than internal energy, to which it is related. At a constant pressure and with work limited to pressure–volume work, the heat of reaction (qp) is equal to the enthalpy change (ΔH)

qp = ΔH = ΔU + PΔV

The heat of combustion (ΔH c0) is the energy released as heat when a substance undergoes complete combustion with oxygen. The chemical reaction for combustion is typically that of a hydrocarbon fuel reacting with oxygen derived from atmospheric air to form gaseous carbon dioxide, water vapor and heat. For example:

methane + oxygen ⇒ carbon dioxide + water vapor

CH4 + 2O2 ⇒ CO2 + 2H2O

13. Types of chemical reactions. Reaction rate. Dependence reaction rate on temperature. Arrhenius equation.

14. Activation energy. Activation energy sources.

Activation energy is defined as the energy that must be overcome in order for a chemical reaction to occur. Activation energy may also be defined as the minimum energy required to start a chemical reaction. The activation energy of a reaction is usually denoted by Ea and given in units of kilojoules per mole.

Activation energy can be thought of as the height of the potential barrier (sometimes called the energy barrier) separating two minima of potential energy (of the reactants and products of a reaction). For a chemical reaction to proceed at a reasonable rate, there should exist an appreciable number of molecules with energy equal to or greater than the activation energy.

At a more advanced level, the Arrhenius Activation energy term from the Arrhenius equation is best regarded as an experimentally determined parameter that indicates the sensitivity of the reaction rate to temperature. There are two objections to associating this activation energy with the threshold barrier for an elementary reaction. First, it is often unclear as to whether or not reaction does proceed in one step; threshold barriers that are averaged out over all elementary steps have little theoretical value. Second, even if the reaction being studied is elementary, a spectrum of individual collisions contributes to rate constants obtained from bulk ('bulb') experiments involving billions of molecules, with many different reactant collision geometries and angles, different translational and (possibly) vibrational energies - all of which may lead to different microscopic reaction rates.

15. Chain reactions. Branching and nonbranching chain reactions. Mechanisms of chain reactions. Examples.

16. Branched-chain explosions.

16.The complete time-history of a spatially homogeneous, constant volume model of self-initiatedbranched-chain explosion including high temperature dissociation arid recombination is examined. This model is motivated by characteristic chemical kinetic steps that are known to occur in H₂-O₂ systems. The kinetic scheme consists of high activation energy/initiation and chain-branching reactions, a zero activation energy gas phase termination reaction, a high activation energy dissociation reaction and a zero activation energy recombination reaction. Perturbation techniques and asymptotic methods are employed to find the transient response of the system temperature and species concentrations, when the high activation energy limit is valid. The chain branching explosion time is defined by very rapid growth of the chain carriers with little change in temperature. It is found that the slow initiation reactions delay the chain branching explosion time significantly compared to that found in simple reactive systems. Subsequently, we find the major part of the thermal explosion where the temperature rises to a maximum value higher than the adiabatic explosion temperature. This difference results from the compression heating in a finite volume. Then the temperature decreases to its final equilibrium value due to the endothermic dissociation reaction.

17. Thermal explosions.

Thermal explosions

In combustion, the definition has been specialized to describe the spontaneous

development of rapid rates of heat release by chemical reactions in initially nearly

homogineous systems. In addition to the branch-chain explosions just discussed, there are

trermat explositns, which do not require complex kinetics for their explanation but instead

can be understood on the basis of a one-step approximation for the chemical reactions. Since

overall rates of chemical reactions generally increase with increasing temperature, the heat

released from an exothermic process may accelerate the rate by raising the temperature of the

reacting mixture. The increased rate of reaction further increases rate of heat release, leading

to a rapid, buildup of thermal energy in the system. The importance of the dependence of the

rate upon temperature distinguishe it hermal explosions from branch-chain explosions, which

may occur in isothermal systems.

For the thermal explosions heat is simultaneously cause and effect of the reaction.

Similarity, a decrease in temperature causes the loss to exceed the generation, so that

temperature of the mixture dicreases further. Thus, at small mixture temperature, there exists

one stable state, and a steady, slow reaction is possible.

If temperature is large enough, then there is no intersection; the generation rate (a) then

always exceeds the lossiate (curve e), causing T to increase with time, as is qualitatively

anticipated during a thermal explosion. The value of temperature fot the occurrence of

thermol explosionmay therefore be identified as the value for which the line (e) is tangent to

the curve (a) - point 3.

For another conditions, for example when surface of a vessel has another value, the heatloss

will be line (d), and thermal explosion may be identifred in point 3'. Therefore

temperature of thermal explosion is not a physical constant.

18. The flame propagation in a pipe. Flame propagation velocity. Normal

flame velocity. Critical diameter. Three zones of a flame propagation in a pipe.

19. Flammable limits. Maximal flame propagation velocity.

Date: 2016-03-03; view: 966