Label this diagram with the correct terms.

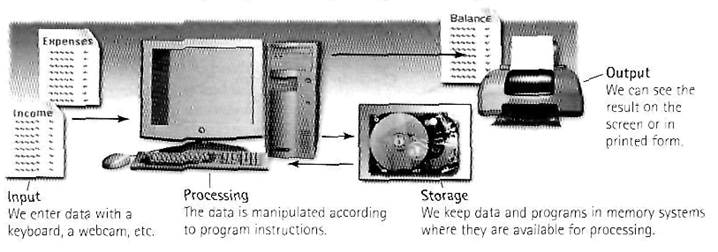
A typical PC

Parts of a computer

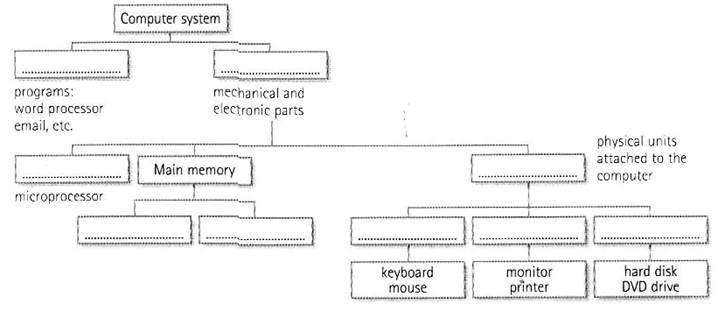
A computer is an electronic machine that accepts, processes, stores and outputs information. A typical computer consists of two parts: hardware and software.

Hardware is any electronic or mechanical part of the computer system that you can see or touch.

Software is a set of instructions, called a program, which tells a computer what to do.

There are three basic hardware sections.

1 The CPU is the heart of the computer, a microprocessor chip which processes data and coordinates the activities of all the other units.

2 The main memory holds the instructions and data which are being processed by the CPU. It has two main sections: RAM (random access memory) and ROM (read only memory).

3 Peripherals are the physical units attached to the computer. The include: Input devices, which let us enter data and commands (e.g. the keyboard and the mouse). Output devices, which let us extract the results (e.g. the monitor and the printer). Storage devices, which are used to store information permanently (e.g. hard disks and DVD-RW drives). Disk drives are used to read and write data on disks. At the back of a computer there are ports into which we can plug external devices (e.g. a scanner, a modem, etc.). They allow communication between the computer and the devices.

Functions of a PC: input, processing, output, storage

Task 1

Read these quotations and say which computer essential they refer to.

1 'Accelerate your digital lifestyle by choosing a Pentium at 4.3 GHz.' processing

2 'Right-click to display a context-sensitive menu.' input

3 'You will see vivid, detailed images on a 17" display." output

4 'This will produce high-quality output, with sharp text and impressive graphics.' output

5 'Use it when you want to let the grandparents watch the new baby sleeping.' input

6 'Press any key to continue." input

Task 2

Match the terms with their definitions.

1 CD/DVD drive a any socket into which a peripheral device may be connected

2 speaker b device used to produce voice output and play back music

3 modem c mechanism that reads and/or writes to optical discs

4 port d device that converts data so that it can travel over the Internet

Task 3

Label this diagram with the correct terms.

Task 4

Date: 2016-03-03; view: 6094