Quartiles, percentiles and correlation coefficients

Now I want to tell how I can use quartiles, percentiles and the correlation coefficient.

Quartiles need to show the lowest and the highest amount of money which person can spend per night. If you use it, you can have more certainty in the future forecast.

Quartiles are one means of identifying the range within which most of the values in the population occur. The lower quartile is the value below which 25% of the population fall and the upper quartile is the value above which 25% of the population fall.

The 25th percentile is also known as the first quartile (Q₁), the 50th percentile as the median or second quartile (Q₂), and the 75th percentile as the third quartile (Q₃). A percentile (or a centile) is a measure used in statistics indicating the value below which a given percentage of observations in a group of observations fall. (http://en.wikipedia.org/wiki/Percentile)

In my research I will use the Q1 because it has R more than 0.5.

Correlation

Correlation is the relationship between two variables (in our case it is expenditure per night and nights). The degree between two variables can be measured and we can decide, using actual results in the form of pairs of data, whether two variables are perfectly or partially correlated, and if they are partially correlated, whether there is a high or low degree of partial correlation. Correlation can be positive (low values of the other and high values of one variable are associated with high value of the other) and negative (low values of the other, and high values of one variable with low values of the other).

However, the correlation has limit. The correlation coefficient should be between -1 and +1. If you get a value outside this range you have made a mistake.

The correlation coefficient does not imply causality, that is it may show that two variables are strongly correlated; however it does not mean that they are responsible for each other.

Disadvantages of the correlation coefficient are that it only measures linear relationships between X and Y and for any relationship to exist, any change in X has to have a constant proportional change in Y. If the relationship is not linear then the result is inaccurate. In addition to this the correlation is meaningless if it is about categorical data, such as hair colour or gender. (http://www.talkstats.com/showthread.php/5352-advantages-and-disadvantages-of-correlation-coefficient)

(Figure 9: correlation)

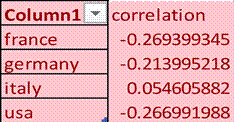
In our case these two variables are expenditures per night and nights. In fact, this table shows that Italy has positive number (low values of the other, and high values of one variable are associated with high value of the other) and other countries have negative numbers (low values of the other, and high values of one variable with low values of the other). The correlation shows that the more nights people stay the more they spend.

UK Study Tours’ data to explore market opportunity to translate the site

Date: 2016-01-14; view: 3172