Standard Error of the Residual

https://www.youtube.com/watch?v=snG7sa5CcJQ

To overcome the difficulty with the correlation coefficient, one can examine the standard error term of an experiment. Recall e_h is the difference between the actual measurement at and the predicted value f( ) using the β coefficients. One can assess the standard deviation of the error terms e_h , and interpret its size.

is called the standard error of the residuals or the residual error. The good thing about the standard error of the residuals is that it is easily interpreted, since it is expressed in the units of the response y. Basically, any predicted value is accurate to at 66.7% confidence, and accurate to 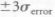at 99.7% confidence (ignoring any experimental measurement error as reflected by S_T). Also, again, most DOE software and spreadsheet programs include this coefficient as an output with any regression analysis.

If replicates were used in the experiment, then the error of the residual can also be compared against the experimental error s_T. If they are of the same size, then the discrepancy between the model and the data is experimental.

T Test

https://www.youtube.com/watch?v=J_o2XiBj5t4

A statistical test of use in regression is the t test, used to determine significance of experimental variables. It is a method to compare two populations and predict if they have essentially the same mean, using a measure over the two distributions called the t-statistic, or t-test. As an example, we can use a t test to determine whether the average of a part dimension is different for sample measurements taken before and after a treatment. In the DOE regression context, the t - test can be used to compare each variable's variance with the residual error ( ) or the experimental error (s_T). Thus, we can predict whether each variable is useful in the prediction. The t-statistic compares the values of the average response at different levels of a variable to the residual error. If this difference is large, then the variable has an effect on the response that is much larger than the residual error, and so the variable is important. Mathematically:

where s_βi, is the standard error of the β_i coefficient, as defined below.

The t-statistic is equivalent in interpretation to the standard deviation multiplier needed to make a normal distribution with mean zero and standard deviation of one become the normal distribution of the data. The interpretation corresponds to the number of standard deviations that the design variable's β is from being zero. A high t-statistic indicates that we are highly confident that the β_i is not zero; a low t-statistic indicates that we are not confident if β_i zero or not.

The t-statistic can also be directly converted into a probability a, using the cumulative probability function for a normal distribution of mean zero and standard deviation one. This number is useful in determining our confidence level. It is the probability that the β_i coefficient is actually zero, and so the variable has no effect. It is a confidence factor, on a probability scale of 0-1 .

Again, most DOE software and spreadsheet programs include both the t-statistic and the confidence factor as an output with any regression analysis. Be aware, though, that some systems indicate the probability that β_i is zero; others indicate the probability that β_i is not zero.

Main effect variables that have low β_i coefficients will also have low slopes on the response diagrams. The probability calculation of the t test provides a confidence factor a on this decision. Variables that have low confidence a should be dropped from the regression analysis. They are indistinguishable from the experimental error.

Another indicator often provided in statistical software during regression analysis is the standard error of the coefficient for each β_i. That is, an indicator s_bi is shown for each β_i. One might think that these error values can be used in the predictor equation:

and propagate onto the variances of y, considering β_i as really being .-This is not correct, as these , terms are not independent error terms. They are simply the standard error of the residual as projected onto the d_i variable. Explicitly, the 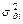terms are given by the diagonal terms of the coefficient covariance matrix, where

where depending on if we are considering residual error or experimental error. Note the , terms are the diagonal terms of In the special case of two factorial experiments with normalized design variables, then Eq. (18.44) reduces to:

where, again, . This becomes clearly evident when one uses normalized variables. The standard error of each coefficient β_i is identical for the same number of levels. It can be confusing, however, when using non normalized data, as then each , value is different for each design variable d_i. They are not independent, however; they are just different scaled versions of the same number, the standard error of the residual 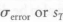. On the other hand, the standard error and the t-statistic are related by Eq. (18.42).

Date: 2016-01-14; view: 653