Experimental Formulation

Let's now consider, more closely, the third step of the experimental design procedure. First we restrict the design variable choices to a number of levels (values), usually two or three levels. This restriction approximates D with, say, 2ⁿ possible (factorial) experimental arrangements for two levels on each variable. It also presumes a model fit between the levels (linearity for two levels and quadratic for three levels). An experiment using two levels for all n design variables is termed a 2ⁿ factorial design: 2ⁿ tests are needed, in this two-level experimental approach, to study all combinations of design variables.

For most physical tests, two or three levels are sufficient to estimate the performance relationship as a function of the design choices. Very few factorial designs use more than three levels to empirically model products or processes. Practically, it is difficult to experiment with more levels since the number of experimental trails increases exponentially, to the nth power of the number of levels.

Statistically, the analysis is easier when we use normalized variables. That is, after approximating the range of a variable with a finite number of points, we denote the lowest level by d_low and the highest level by d_high. These levels are the boundaries for each design variable and are then mapped to a normalized domain with span[ -1, + 1]. This -1 to + 1 range is a normalized representation of each design variable. For two-level experiments, we denote the higher value of d_i with a (+ 1) and the smaller value with a (-1), where a value of (0) represents the midpoint of the range. If , we think of as a normalized scale for d_i, from a transformation:

and the inverse:

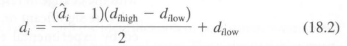
If d_i simply represents a binary decision, such as "use vibration isolation, do not use vibration isolation," then there is no implied scale associated to the range between numbers (+ 1) and (-1). The extremes are the only points of interest. For the remainder of this chapter, we will shorten the notation of to d_i and consider all design variables as normalized.

http://www.youtube.com/watch?v=7wAYUcRPBI4

Date: 2016-01-14; view: 698