Basics of Designed Experiments

Physical Models and Experimentation

Consider the redesign of a coffee mill. Most mills are notoriously loud, generating over 80 dB of noise, even though they are intended for use during the early morning hours. To explore noise absorption and reduction, an analytical model could be developed to representation how vibrations are generated, transmitted, and emitted to the acoustical environment. The resulting model could then be used to change the mill's dimensions for noise reduction. To be sufficiently accurate, the modeling effort would require significant time resources, in addition to an in-depth knowledge of the field.

I. CHAPTER ROADMAP

The material in this chapter is diagrammed in Figure 18.1.

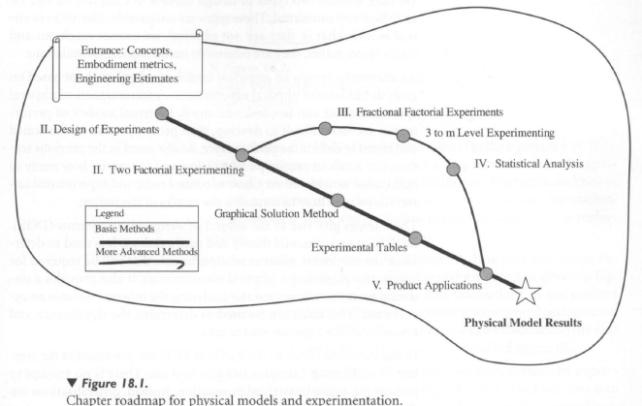
II. DESIGN OF EXPERIMENTS

https://www.youtube.com/watch?v=uAnziknkQXw

We have studied two types of design models in Chapters 13 and 16: analytical and numerical. These types are commonly referred to as virtual models, that is, they are not physical, we cannot reach out and touch them; rather, they are ostensibly mathematical formulations. An alternative type is an empirical model, one developed not based on analysis but instead physical experiments-measurements of physical systems that we can see, feel, and smell. If virtual models of performance are too difficult to develop, then prototypes can be fabricated and tested to determine performance. As discussed in the previous section, key issues in prototype fabrication and testing are how many to build, what variables to vary, how to control noise and experimental uncertainties, and how to formalize the results of the testing.

These issues give rise to the subject of design of experiments (DOE). DOE is an experimental theory and methodology. It is used to determine the minimum number of experiments that will be required for adequately predicting a physical phenomenon. It also provides a statistical basis for monitoring and analyzing the inherent noise in an experiment. This basis can be used to determine the significance and relevance of the experimental results.

Basics of Designed Experiments

As design experimenters, we are experimentally optimizing our identified design using physical models. Out of the possible design choices for a concept, we experimentally determine which combinations are the most preferred. Our goal is not to fit a model to the experiments for the sake of observation. Instead, we are answering the questions of, "What are the preferred choices for the product?" and "What are the most sensitive choices for maximizing the performance of the product?"

We start our discussions on design of experiments here with the concept of a formal engineering model, as introduced in Chapter 13. A design space D and a performance metric(s) p are identified for modeling a product. The problem addressed by DOE concerns the existence of no formal analytical or numerical relationship for representing p as a function of the de 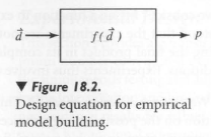sign variables dÎD. We have no expression fin the equation 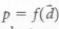.Figure 18.2 illustrates the abstract relationship between the product performance metric and the design variable choices. The inputs are known, and the metric for measuring the output is chosen. We need the machinery in the box to relate d to p, resulting in a means to estimate the performance.

More generally, as introduced in Chapter 13, there are other factors beyond design variables that can affect the performance p, as shown in Figure 18.3. Manufacturing variations and fluctuations in the product environment can lead to differences in customer experienced performance, represented as noise nÎN. These other factors are discussed in the next chapter; for now we restrict our study to the model of Figure 18.2.

As depicted in Figure 18.2, we can estimate performance by experimentally determining a phenomenological model. The basic idea is to "fit" a relationship f over D using statistical concepts of measured performance states. Based on this function fit, we can then experimentally maximize f over D and determine the most sensitive design variables. In Chapter 19, this approach is augmented by simultaneously considering the effect of noise variables on product performance (Figure 18.3).

Date: 2016-01-14; view: 809