Give an example Model Checking for LTL. Automata approach to the verification of formulas LTL. Path calculations and Kripke structures.

Kripke structure - a state machine with marked transitions, each state is associated a set of atomic propositions are true in this state

Kripke structure - the system transitions with marked conditions and marked transitions

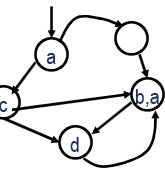
Scan Kripke structure defines an endless chain of states - the possibility of computing

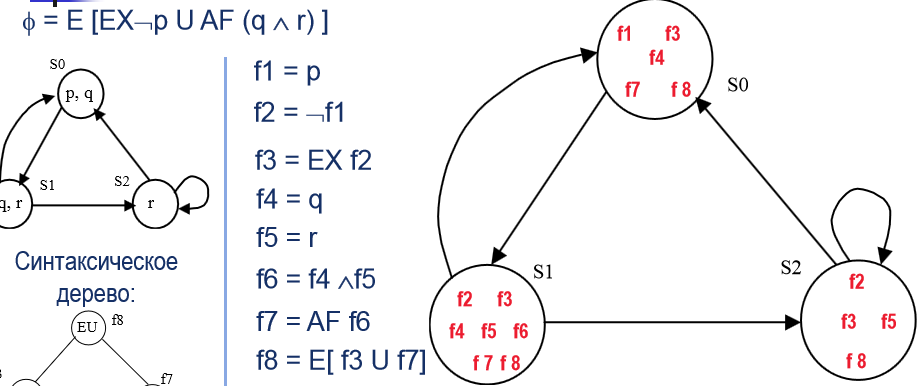
For LTL example

GFq - always in the future

Fq - at least once in the future

F q - never in the future

GFq - infinitely many times in the future

FGq - to a certain point, constantly

p->Fq - on the river in the response q s0 will sometime in the future

G [p->Fq] - always on the river will be the response q

24. What is Buchi automata – finite model work of languages. Control automation.

Kriple structureàBuchi automata

Some properties of the systems do not express CTL-formulas, but expressed LTL-formulas. Thus the need for, and feasibility of such algorithms are formulas on Kripke structure

To check whether the model of the formula logic LTL, built machines Buchi AM is checked emptiness language accepted by the automaton Buchi - synchronous composition of process

Theorem. For every LTL formula exists Buchi automaton, which is a model of the formula (t.e.dopuskaet the same language, which is defined by the formula LTL)

Theorem. There Buchi machines, for which there is no formula LTL, describing the language that allowed these guns

How to verify that the language that allows Buchi automaton A is not empty?

Theorem . Buchi automaton A admits a non-empty string TTOGDA when A contains a reachable from the initial state of the SSC, which includes at least one final state

NECESSITY .-Let A permit p. Then, as p w-chain A contains a reachable final state s, which takes place under the influence of p infinite number of times. All states A, which was held in A under the influence after the first visit p s, form achievable SSC.

ADEQUACY.-Let A FCS contains R, reachable from the initial state and a final state s R. Then it s can be achieved in an infinite number of times A

Machine A has a language with a finite number b, and an infinite number of a

Machine B may take the language with a finite number a and an infinite number of b

The intersection of these languages is empty (no infinite chains of a and b, including a finite number, and a, and b are

Date: 2016-01-03; view: 2610