Competitive Inhibition

Consider the following system

(14.33)

where an inhibitor, I, binds reversibly to the enzyme at the same site as S. S-binding and I-binding are mutually exclusive, competitive processes. Formation of the ternary complex, EIS, where both S and I are bound, is physically impossible. This condition leads us to anticipate that S and I must share a high degree of structural similarity because they bind at the same site on the enzyme. Also notice that, in our model, EI does not react to give rise to E + P. That is, I is not changed by interaction with E. The rate of the product-forming reaction is v = k₂[ES].
It is revealing to compare the equation for the uninhibited case, Equation (14.23) (the Michaelis-Menten equation) with Equation (14.43) for the rate of the enzymatic reaction in the presence of a fixed concentration of the competitive inhibitor, [I]

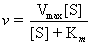
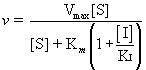
(see also Table 14.6). The K_m term in the denominator in the inhibited case is increased by the factor (1 + [I]/K_I); thus, v is less in the presence of the inhibitor, as expected. Clearly, in the absence of I, the two equations are identical. Figure 14.13 shows a Lineweaver-Burk plot of competitive inhibition. Several features of competitive inhibition are evident. First, at a given [I], v decreases (1/v increases). When [S] becomes infinite, v = V_max and is unaffected by I because all of the enzyme is in the ES form. Note that the value of the -x-intercept decreases as [I] increases. This -x-intercept is often termed the apparent K_m (or K_mapp) because it is the K_m apparent under these conditions. The diagnostic criterion for competitive inhibition is that V_max is unaffected by I; that is, all lines share a common y-intercept. This criterion is also the best experimental indication of binding at the same site by two substances. Competitive inhibitors resemble S structurally.

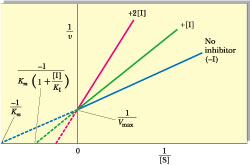
Figure 14.13 • Lineweaver-Burk plot of competitive inhibition, showing lines for no I, [I], and 2[I]. Note that when [S] is infinitely large (1/[S]50), Vmax is the same, whether I is present or not. In the presence of I, the negative x-intercept521/K_m(11[I]/K_I).

A Deeper Look

The Equations of Competitive Inhibition Given the relationships between E, S, and I described previously and recalling the steady-state assumption that d[ES]/dt = 0, from Equations (14.14) and (14.16) we can write (14.34) Assuming that E + I ⇌ EI reaches rapid equilibrium, the rate of EI formation, vf' = k3[E][I], and the rate of disappearance of EI, vd' = k-3[EI], are equal. So, (14.35) Therefore, (14.36) If we define KI as k-3/ k3, an enzyme-inhibitor dissociation constant, then (14.37) knowing [ET] = [E] + [ES] + [EI]. Then (14.38)

Solving for [E] gives (14.39) Because the rate of product formation is given by v = k2[ES], from Equation (14.34) we have (14.40) So, (14.41) Because Vmax = k2[ET], (14.42) or (14.43)

Date: 2016-01-03; view: 801