Description of laboratory research facility and methodology of measurements

Devices and outfits: Set of inductances, set of capacities, set of resistances, voltmeter, sound generator ГЗ-36.

In a given work we study capacitor, inductor and resistor voltages dependencies on external driving EMF frequency Ω. Magnitudes of R, C, L and amplitude of driving EMF E_m remain constant during the work.

Facility's scheme represented on Fig.13. There we have capacitor C (one value from the set of capacities), inductor L (one value from the set of inductances) and resistor R (one value set on resistance box). The real inductance L has its own active resistance R_L. Such inductance is equivalent to series RL circuit. As driving EMF source we have ГЗ-36 generator (or any similar). It output voltage (i.e. EMF e) can be measured with help of built-in voltmeter. Note that voltmeter indicates effective voltage magnitude, not amplitude. Effectivecurrent (voltage) magnitude is such magnitude of direct current which produces same heat in same circuit that alternating current does by the time of a period. Effective current is also called root mean square (RMS) value of alternating current. For harmonic alternating current relations between effective and amplitude values are so:

,

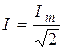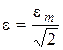
Obviously that effective current and EMF related as

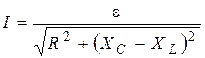
If we’ll change the frequency of generator then phase lag between current and EMF also will be changed as the reactance changes. As it seen from (63), (64) and Fig.13, at low frequencies u_L < u_C and u_L > u_C at high. Obviously that there will be some frequencies Ω_C = Ω_L at which u_C = u_L and get maximum.

Using indexes of voltmeter, switched to capacitor or inductance coil we can find frequency Ω_C or Ω_L, which, in case of high enough quality, will be equal to resonance frequency.

So, in this work we can plot:

a) Effective voltage on capacitor U_C versus driving EMF frequency Ω = 2πν, where ν determined with ГЗ-36 limb;

b) Effective current I = 2πνCU_C in a circuit versus Ω;

c) Effective voltage on inductor U_L = IΩL, or substituting I and Ω, U_L = 4π²ν²CU_CL. Inductance L can be determined from the match of driving and natural frequencies of the circuit at resonance, i.e.:

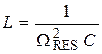
4 Data processing (see laboratory work № 4-1).

Date: 2015-12-24; view: 832