
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
EXPLORING of HARMONIC OSCILLATIONS
1 Goal of the work:
1. Studying physical pendulum undamped oscillations description method.
2. Studying a moment of inertia and equivalent length of physical pendulum determination method.
Main concepts
Oscillations (including vibrations and variations) are processes changes of state that are repeated more or less regularly with time. There are many kinds of oscillations, not only mechanical. Any physical quantity makes oscillations if it repetitively varies in opposite directions near some of its value.
A motion of a mechanical system near its equilibrium position, during which the system passes through an equilibrium position over and over in opposite directions is being termed mechanical oscillations.
A state of a system, left by its own, in which it can stay indefinitely long without any motion, is called equilibrium state.
Free oscillations (simple harmonic and dumped oscillations) are ones that occur in absence of externally applied variable action on the system. Forced oscillations are ones set up in system as a result of variable external effects (periodic external force in mechanical systems or generator’s alternating emf in electromagnetic systems).
Simplest model of oscillatory system is called a harmonic oscillator. When the oscillatory system not looses energy, it is being described by homogeneous second order differential equation that is termed equation of harmonic oscillator in differential view:
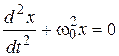 or
or 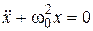 . (1)
. (1)
A motion of such system is termed simple harmonic and the oscillating physical quantity x varies under sine or cosine law. Thus general solution for this differential equation (1) will be equation of simple harmonic oscillations:
x(t)=A×cos(ω0t+φ0) or x(t)=A×sin(ω0t+φ0+ π/2), (2)
where x(t)=f(t) – value of oscillating quantity at the time t is called in mechanical systems as displacement (relatively to equilibrium position).
Constant A, which is equal to the largest absolute value of oscillating physical quantity, is called the amplitude of oscillations. Amplitude measurement unit is a same, as measurement unit of a quantity x.
Expression
ω0t+φ0 = Φ(t), (3)
which defines the magnitude of quantity x at given moment of time, is called the phase of oscillation.
SI measurement unit for phase is radian - [rad].
At initial moment of time (t =0) phase Φ is equal to initial phase φ0:
Φ(t=0)= φ0,
When we deviate the pendulum at the first time to the left, then
x=x(t=0)= –A and j0 =p, (4)
but when we deviate the pendulum at the first time to the right, then
x0=x(t=0)=+A and j0=0. (4a)
Differentiation of (3) gives:
 , (5)
, (5)
hence, cyclic frequency is the time rate of change (velocity of variation) of a phase that measurement unit is radians per second - [rad/s].
Parameters of oscillations:
The period of the oscillations T is the smallest interval of time after which repeat all values of physical quantities characterized oscillatory motion. One full oscillation completes by the time of period T.
Frequency is defined as a number of oscillations per unit time:
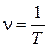 (6)
(6)
SI measurement unit for frequency is Hertz – [Hz].
One full oscillation's phase cycle corresponds to 2π radians (as period of harmonic function). Then cyclic frequency (5) of oscillations is the number of phase cycles per seconds:
 (7)
(7)
SI measurement unit for cyclic frequency is radians per second – [rad/s].
Then the period of the oscillations
 (8)
(8)
SI measurement unit for period is second – [s].
Date: 2015-12-24; view: 1130
| <== previous page | | | next page ==> |
| LIST OF LABORATORY WORKS | | | Harmonic oscillations of physical pendulum |