
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
DIAGRAMA FASORIAL DEL GENERADOR DE INDUCCION











 I2 I2sx2 sE2 y2s Im Ih+e If V1 I1 E1 I1r1 I1x1 -I2
I2 I2sx2 sE2 y2s Im Ih+e If V1 I1 E1 I1r1 I1x1 -I2
DETERMINACION DE PARAMETROS
Los seis parámetros del motor de inducción (r1, x1, r2, x2 Gm (Rm), Bm (Xm)) pueden determinarse a partir de las siguientes pruebas:
· Medición de Resistencia (aplicable a los devanados del
estator)
· Prueba de Vacío (Prueba de Vacío Ideal)
· Prueba de Rotor Bloqueado
MEDICION DE RESISTENCIA.-
Existen dos métodos para medir la resistencia en un circuito:
a) Método Indirecto: Voltímetro-Amperímetro (caída de tensión)
b) Medición Directa: Utilizando equipos de medición de resistencia. En este método se puede utilizar:
 Óhmetros
Óhmetros
Puentes de Resistencia Kelvin
Wheastone
a) Método Voltímetro-Amperímetro.-
Se aplica una tensión c.a. que debe ser igual o menor que la tensión nominal, pero no puede ser mayor que ésta.
Se coloca un voltímetro y un amperímetro en cada conexión, como indica el gráfico y luego se miden las resistencias:
 |  |
Y Rmedida = V/A = 2R D Rmedida = V/A = R(2R)/(R+2R)
R = ½ V/A = ½ Rmedida R = 3/2(V/A) = 3/2 Rmedida
PRUEBA DE VACIO.-
Durante esta prueba se aplica Voltaje 3f y frecuencia (nominales) y no se conecta ninguna carga en el eje. Circula una corriente por fase I0, y se toman las lecturas de las mediciones siguientes:
(a) La tensión primaria por fase V1 que es igual usualmente a la tensión nominal;
(b)La corriente por fase primaria I0,
(c) La potencia de entrada P0.
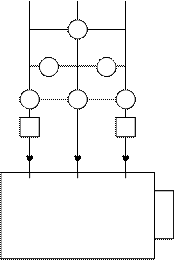 |
La potencia P0 (Potencia 3f activa) es igual a las pérdidas del motor en vacío. Estas son las pérdidas en el cobre m1I02r1 en el arrollamiento del estator, las pérdidas por histéresis y corrientes de Foucault Ph+e debidas al flujo principal, las pérdidas por fricción y ventilación del rotor PF+V y las pérdidas en el hierro debidas a la rotación y a la abertura de las ranuras.
Ya que la componente activa de I0 es pequeña en comparación con su componente reactiva If, el factor de potencia en vacío Cosj0 = P0/(m1V1I0) es pequeño también, alrededor de 0.05 a 0.15.
Es necesario tomar en cuenta únicamente una corriente del rotor muy pequeña, y puede considerarse abierto el circuito secundario. Esto puede deducirse de la magnitud de la resistencia que representa la potencia mecánica del rotor, y esta resistencia viene a ser muy elevada debido a que el deslizamiento en vacío es despreciablemente pequeño, esto es, el circuito del rotor está prácticamente abierto en vacío. Entonces, el circuito equivalente está representado como sigue:
PRUEBA DE VACIO IDEAL.-
Consiste en acoplar la máquina de inducción a una máquina auxiliar y que la lleve a la velocidad sincrónica igual a la velocidad de la máquina. Ambas máquinas deben girar en el mismo sentido.
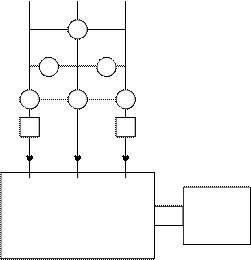 |
Con la prueba de vacío ideal se consigue que la máquina auxiliar entregue a la máquina sincrónica las pérdidas PF+V y Pfe rot.
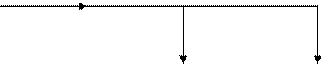 |
P0 = m1V1I0Cosj0
m1I02r1
Pcu1 Ph+e
 P0 = m1V1I0Cosj0 + Ph+e Ph+e = P0 m1I02r1
P0 = m1V1I0Cosj0 + Ph+e Ph+e = P0 m1I02r1
V1 Iox1 » E1
V1 = -E1 + I0r1 + jI0x1

Gm = Ph+e /(m1E12)
Im = Ih+e + If ; I0 = Im
Ih+e = E1Gm
If = I0 Ih+e

Bm = If/E1

Xm = E1/I0

Rm = Gm/(Gm2 + Bm2) » Gm/Bm2» GmXm2
De este modo, la prueba de vacío produce los parámetros del flujo principal, a condición de que la reactancia primaria de dispersión x1 sea conocida.
PRUEBA DE ROTOR BLOQUEADO.-
Esta prueba es similar a la prueba de corto circuito de los transformadores.
Durante esta prueba se frena el rotor, y la máquina de inducción se alimenta con un voltaje reducido 3f para tratar de hacer circular una corriente nominal, pero si esto no es posible, la corriente debe aproximarse al valor nominal.
 |
En reposo, el deslizamiento s es igual a 1, y el circuito equivalente del motor es el siguiente:
Ya que la impedancia secundaria r2+jx2 es menor en comparación con Xm y la caída de tensión primaria es grande, sólo fluye una pequeña corriente por el circuito del flujo principal y también las pérdidas en el hierro debidas a dicho flujo son pequeñas.
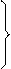 VL
VL
IL CosjL = PL/(m1VLIL) (fp en reposo > fp en vacío)
PL
Las cantidades medidas PL, VL e IL determinan la impedancia de cortocircuito ZL, la resistencia de corto circuito RL y la reactancia de corto circuito XL.
ZL = VL/IL PL = m1IL2RL RL = PL /(m1IL2)
XL = [ ZL2 RL2 ]1/2
 RL = r1 + r2
RL = r1 + r2
r2 = RL r1
 XL = x1 + x2 ; x1 » x2
XL = x1 + x2 ; x1 » x2
XL/2 = x1 = x2
Con este valor de x1 se pueden determinar los parámetros del flujo principal Xm y Rm.
Date: 2015-12-24; view: 1020
| <== previous page | | | next page ==> |
| CURVAS NORMALIZADAS | | | DIAGRAMA CIRCULAR DEL MOTOR POLIFASICO DE INDUCCION |