CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
RELACIONES DE POTENCIA Y PAR MOTOR
POTENCIA MECANICA Y PAR MOTOR DESARROLLADOS:
E2’ = I2’r2’/s +jI2’x2’ (Ecuación de Kirchhoff del Rotor)
Multiplicando ambos miembros por la corriente I2’ del rotor y el número de fases m1 nos conduce a expresiones para la característica de potencia mecánica desarrollada queda la siguiente expresión:
m1I2’E2’ = m1I2’2r2’/s + jm1I2’2x2’
Donde:
m1I2’E2’: Potencia Total
m1I2’2r2’/s: Potencia Electromagnética o Potencia de Campo
Giratorio (Pcgir)
m1I2’2x2’: Potencia Reactiva Estator Rotor Pcgir
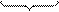
Pentrada PSalida Pcu1 Ph+e Pcu2 PF+V Pfrot
Entrehierro
Pmdes: Potencia Mecánica Desarrollada
Pmdes = Pcgir - Pcu2
Pmdes = m2I2’r2’/s – m2I2’2r2’ = m2I2’2r2 (1-s)/s
Estas ecuaciones se deducen también del circuito equivalente, debido a que éste ha sido deducido de las ecuaciones fundamentales.
Pcgir = m1I2’2r2’/s = Pcu2/s
Pcu2 = sPcgir
s = Pcu2/Pcgir
Pmdes = Pcu2(1-s)/s
Pcu2 = Pmdes [s/(1-s)]
Pmdes = Pcgir(1-s)
Pcgir = Pmdes/(1-s)
Usando la relación básica de la mecánica:
T = 7.04P/n [lb-pies]
Puede deducirse la expresión del torque desarrollado utilizando la ecuación de Potencia de campo giratorio y sustituyendo n por la velocidad ns en la ecuación anterior, debido a que el flujo tiene una velocidad constante ns.
Entonces se tiene que:
Tdes = 7.04Pcgir/ns = 7.04m1I2’2r2’/sns
Tdes = 7.04Pmdes/n
El Torque desarrollado NO es el torque que está en el eje.
En los motores de inducción:
Si s = 0 Sincronismo
Si s = 1 Reposo
sn (Deslizamiento nominal) puede tener rangos desde 0.01 hasta 0.05.
En la figura se muestran tres formas diferentes de características par motor-velocidad de motores jaula de ardilla. El diseño A es el del motor de propósito general, que muestra un par motor máximo a un deslizamiento definido. C y D son máquinas especiales diseñadas para tener altor pares motores de arranque, esto es, altos pares motores en estado estacionario (n = 0).
TORQUE MAXIMO:
Analizando los circuitos equivalentes del motor de inducción:
Aplicando el Teorema de Thévenin:
| I2’ = Vth/[(Rth+r2’/s)+j(xth+x2’) I2’ = Vth/ [(Rth+r2’/s)2+(xth+x2’)2]1/2 T = 7.04m1{Vth2/[(Rth+r2’/s)2+(xth+x2’)2]}r2’/nss dT/ds = 0 sTmax = ± r2’/ [(Rth)2 +(xth+x2’)2] 1/2 Tmax = 7.04m1Vth2/2ns [Rth + [Rth2 +(xth+x2’)2] 1/2] Motor Tmax = 7.04m1Vth2/2ns [ [ Rth2 +(xth+x2’)2– Rth ] Generador Otra forma: |
I2’ = V1/[(r1+r2’/s)+j(x1+x2’)
I2’ = V1/ [(r1+r2’/s)2+(x1+x2’)2] 1/2
T = 7.04m1{V12/[(r1+r2’/s)2+(x1+x2’)2]}r2’/n s
dT/ds = 0
sTmax = ± r2’/ [(r1)2 +(x1+x2’)2] 1/2
Tmax = 7.04m1V12/2ns [r1 + [ r12 +(x1+x2’)2 ] 1/2] Motor
Tmax = 7.04m1V12/2ns [ [ r12 +(x1+x2’)2 ] 1/2– r1 ] Generador
Motor
 | |||
 | |||
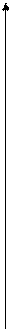Tmax
 |
s =1 s = 0
 | |||
 | |||
Freno Generador
Date: 2015-12-24; view: 755
| <== previous page | | | next page ==> |
| DIAGRAMA FASORIAL Y CIRCUITO EQUIVALENTE DEL MOTOR POLIFASICO DE INDUCCION | | | CURVAS NORMALIZADAS |