
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
INTEGRAL CALCULUS
Problem 1. Find indefinite integrals
1. à) 
| á) 
| â) 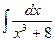
|
ã) 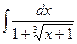
| ä) 
| |
2. à) 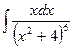
| á) 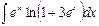
| â) 
|
ã) 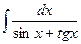
| ä) 
| |
3. à) 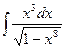
| á) 
| â) 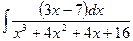
|
ã) 
| ä) 
| |
4. à) 
| á) 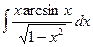
| â) 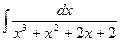
|
ã) 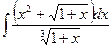
| ä) 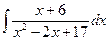
| |
5. à) 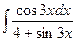
| á) 
| â) 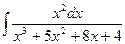
|
ã) 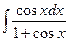
| ä) 
| |
6. à) 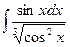
| á) 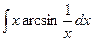
| â) 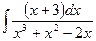
|
ã) 
| ä) 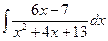
| |
7. à) 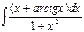
| á) 
| â) 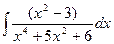
|
ã) 
| ä) 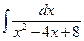
| |
8. à) 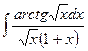
| á) 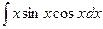
| â) 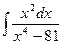
|
ã) 
| ä) 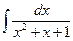
| |
9. à) 
| á) 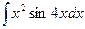
| â) 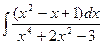
|
ã) 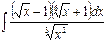
| ä) 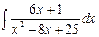
| |
10. à) 
| á) 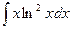
| â) 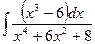
|
ã) 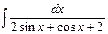
| ä) 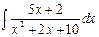
| |
11. à) 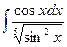
| á) 
| â) 
|
ã) 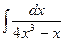
| ä) 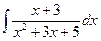
| |
12. à) 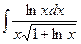
| á) 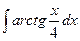
| â) 
|
ã) 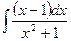
| ä) 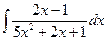
| |
13. à) 
| á) 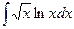
| â) 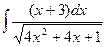
|
ã) 
| ä) 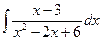
| |
14. à) 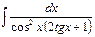
| á) 
| â) 
|
ã) 
| ä) 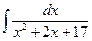
| |
15. à) 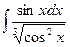
| á) 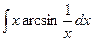
| â) 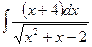
|
ã) 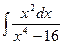
| ä) 
| |
16. à) 
| á) 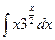
| â) 
|
ã) 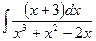
| ä) 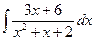
| |
17. à) 
| á) 
| â) 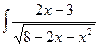
|
ã) 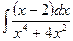
| ä) 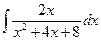
| |
18. à) 
| á) 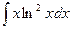
| â) 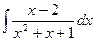
|
ã) 
| ä) 
| |
19. à) 
| á) 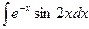
| â) 
|
ã) 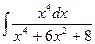
| ä) 
| |
20. à) 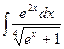
| á) 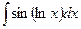
| â) 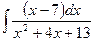
|
ã) 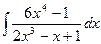
| ä) 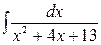
| |
21. à) 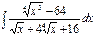
| á) 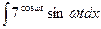
| â) 
|
ã) 
| ä) 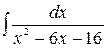
| |
22. à) 
| á) 
| â) 
|
ã) 
| ä) 
| |
23. à) 
| á) 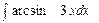
| â) 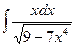
|
ã) 
| ä) 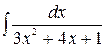
| |
24. à) 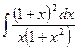
| á) 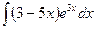
| â) 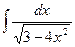
|
ã) 
| ä) 
| |
25. à) 
| á) 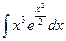
| â) 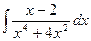
|
ã) 
| ä) 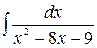
| |
26. à) 
| á) 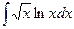
| â) 
|
ã) 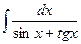
| ä) 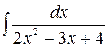
| |
27. à) 
| á) 
| â) 
|
ã) 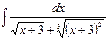
| ä) 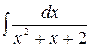
| |
28. à) 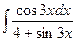
| á) 
| â) 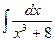
|
ã) 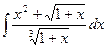
| ä) 
| |
29. à) 
| á) 
| â) 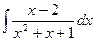
|
ã) 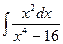
| ä) 
| |
30. à) 
| á) 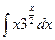
| â) 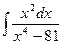
|
ã) 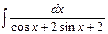
| ä) 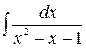
|
Problem 2. Calculate definite integrals
1. à)  á)
á) 
| 16. à) 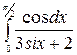 á) á) 
|
2. à) 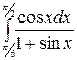 á)
á) 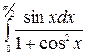
| 17. à) 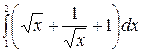 á) á) 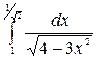
|
3. à) 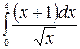 á)
á) 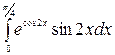
| 18. à) 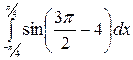 á) á) 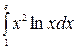
|
4. à) 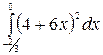 á)
á) 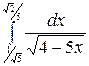
| 19 à) 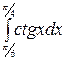 á) á) 
|
5. à)  á)
á) 
| 20. à) 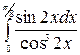 á) á) 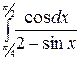
|
6. à) 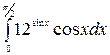 á)
á) 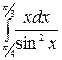
| 21. à)  á) á) 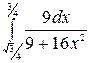
|
7. à) 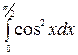 á) á) 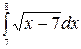
| 22. à) 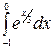 á)
á) 
|
8. à) 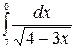 á)
á) 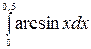
| 23. à)  á)
á) 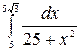
|
9. à)  á)
á) 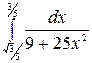
| 24. à)  á) á) 
|
10. à) 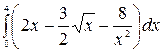 á) á) 
| 25. à) 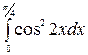 á)
á) 
|
11. à) 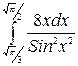 á) á) 
| 26. à)  á)
á) 
|
12. à) 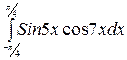 á) á) 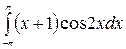
| 27. à) 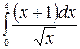 á)
á) 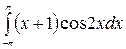
|
13. à) 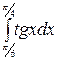 á) á) 
| 28. à)  á)
á) 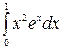
|
14. à) 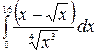 á) á) 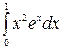
| 29. à) 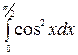 á)
á) 
|
15. à)  á) á) 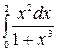
| 30. à)  á)
á) 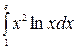
|
Problem 3.
1. Find the area bounded by the curve 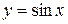 , the x-axis, and the lines
, the x-axis, and the lines  and
and 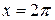 .
.
2. Find the area of the ellipse 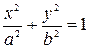 .
.
3. Find the area bounded by the curve  ,
, 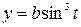 for
for 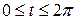 .
.
4. Find the area of the lemniscate  .
.
5. Find the length of the cissoid  from
from 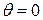 to
to 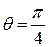 .
.
6. Find the area bounded by the parabola 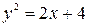 and the straight line
and the straight line  .
.
7. Find the area bounded by the ellipse  .
.
8. Find the area of the ellipse whose parametric equations are 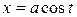 and
and  .
.
9. Find the parabola  from (0,0) to (-4,4).
from (0,0) to (-4,4).
10. Find the area bounded by the parabola 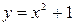 , the x-axis, and the lines
, the x-axis, and the lines 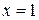 and
and 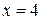 .
.
11. Find the bounded area between the curves 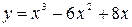 and
and 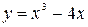 .
.
12. Find the area of an arch of the cycloid 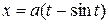 and
and  where
where 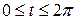 .
.
13. Find the area of the cardioid  .
.
14. Find the area of one loop of the curve 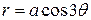 .
.
15. Find the area between the curve 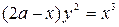 where
where 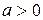 and its asymptote.
and its asymptote.
16. Sketch the graph  and find the area of the loop.
and find the area of the loop.
17. Sketch the graph  and find the area between the curve and its asymptote.
and find the area between the curve and its asymptote.
18. Find the area in the first quadrant between the graph of  , the coordinate axes, and the vertical line
, the coordinate axes, and the vertical line 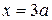 .
.
19. Find the circumference of a circle of radius R.
20. Find the entire length of the hypocycloid 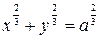 .
.
21. Find the volume of the solid generated by revolving about the x-axis the area bounded by the curve  and the lines x=0 and y=8.
and the lines x=0 and y=8.
22. Find the volume of the solid generated by revolving about the line y=8 the area bounded by the curve  and the lines x=0 and y=8.
and the lines x=0 and y=8.
23. The area bounded by the curve xy=1 and the lines x=1, x=3 and y=0 is evolved about the x-axis. Find the volume generated.
24. The smaller segment cut from the circle 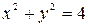 by the line y=1 is revolved about that line. Find the volume generated.
by the line y=1 is revolved about that line. Find the volume generated.
25. Find the volume generated by revolving about the line y=x the area bounded by the line 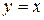 and the parabola
and the parabola 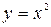 .
.
26. The area bounded by the hyperbola  and the line x=6 is revolved about the y-axis. Find the volume generated.
and the line x=6 is revolved about the y-axis. Find the volume generated.
27. Find the volume generated by revolving about the line x=2, the area bounded by the parabola 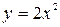 and the line
and the line 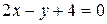 .
.
28. Find the area of the surface generated by revolving the curve  about the initial line.
about the initial line.
29. Find the area of the surface generated by revolving the curve 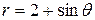 about the line
about the line  .
.
30. Find the area of the surface generated by revolving an arch of the cycloid 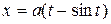 ,
, 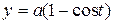 where
where 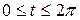 about the x-axis.
about the x-axis.
REFERENCES:
1. Atkinson, K.E. (1993), Elementary Numerical Analysis, 2nd ed., John Wiley (New York).
2. Blachman, N. (1999), Mathematica : a Practical Approach, 2nd ed., Prentice Hall (Upper Saddle River, N.J).
3. Bracewell, R.N. (1986), The Fourier Transform and Its Applications, 2nd ed., McGraw-Hill (New York).
4. Edwards, C.H., Penney, D.E. (1998), Calculus with Analytic Geometry, 5th ed., Prentice Hall (Upper Saddle River, N.J).
5. Efimov N.V. «A short course of analytical geometry». M. 1967.
6. Franklin, J.N. (1968), Matrix Theory, Prentice-Hall (Englewood Cliffs, NJ).
7. Gerald, C.F. (1999), Applied Numerical Analysis, 6th ed., Addison-Wesley (Cambridge, MA).
8. Golub, G.H. (1996), Matrix Computations, 3rd ed., Johns Hopkins University Press (Baltimore).
9. Greenberg, M.D. (1998), Advanced Engineering Mathematics, 2nd ed., Prentice Hall (Upper Saddle River, N.J).
10. Gusak A.A. (1983, 1984), «Higher Mathematics. Tutorial», Minsk. Vol.1, 2.
11. Gusak A.A. (1988), «Problems and exercises in higher mathematics», Minsk.V 1, 2.
12. Hildebrand, F.B. (1974), Introduction to Numerical Analysis, 2nd ed., McGraw-Hill (New York).
13. Hildebrand, F.B. (1976), Advanced Calculus for Applications, 2nd ed., Prentice-Hall (Englewood Cliffs, NJ).
14. Kreyszig, E. (1999), Advanced Engineering Mathematics, 8th ed., John Wiley (New York).
15. Minorsky V.P. (1987), «Problems in higher mathematics». M. Science.
16. Olver, F.W.J. (1974), Asymptotics and Special Functions, Academic Press (New York).
17. O'Neil, P.V. (1995), Advanced Engineering Mathematics, 4th ed., PWS-Kent Pub. (Boston).
18. Piskunov N.S. (1985), «The differential and integral calculus». M. Vol 1, 2.
19. Privalov N. N. (1964), «Analytic geometry», M.
20. Spiegel, M.R. (ed.) (1968), Mathematical Handbook of Formulas and Tables, McGraw-Hill (New York).
21. Shipachev V.S. (2001), «Higher Mathematics», M.
22. Stoer, J., Bulirsch , R. (1993), Introduction to Numerical Analysis, 2nd ed., Springer-Verlag (New York).
23. Strang, G. (1988), Linear Algebra and Its Applications, 3rd ed., Harcourt, Brace, Jovanovich (San Diego).
24. Strang, G. (1991), Calculus, Wellesley-Cambridge Press (Wellesley, MA).
25. Strang, G. (1998), Introduction to Linear Algebra, Wellesley-Cambridge Press (Wellesley, MA).
26. Wang, Z.X. (1989), Special Functions, World Scientific (Singapore).
27. Watson, G.N. (1944), A Treatise on the Theory of Bessel Functions, 2nd ed., Macmillan (New York).
28. Wolfram, S. (1999), The Mathematica Book, 4th ed., Cambridge Univ. Press (New York).
29. Wylie, C.R. (1995), Advanced Engineering Mathematics, 6th ed., McGraw-Hill (New York).
30. Zwillinger, D. (ed.) (1996), CRC Standard Mathematical Tables and Formulae, 30th ed., CRC Press (Bocs Ration, FL).
Date: 2015-01-02; view: 1109
| <== previous page | | | next page ==> |
| Application of the derivative. | | | GOVERNMENT AND POLITICS |