
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
PRACTICAL CLASS ¹ 3-5.
The simplest problem of analytic geometry. Equations of a straight line on a plane. Analytic geometry in space. Vectors. Simple operations with vectors. The scalar, vector and mixed product of vectors
Theoretical questions: 1. How Rectangular Cartesian coordinates are given on the plane?
2. What names have Rectangular Cartesian coordinates axes?
3. What is connection between polar and Rectangular coordinates of points?
4. What formula find a distance between two points?
5. Dividing Formulas of segment in given ratio.
6. Equation of Straight (right) line with angular coefficients.
7. Common equation of Straight (right) line
8. Equation of Straight (right) line with given angular coefficients and passing through a given point.
9. Equation of Straight (right) line passing through given two points.
10. Equation of Straight (right) line in segments.
11. Angle between two lines.
12. The parallelism conditions of two lines.
13. . The perpendicularity conditions of two lines.
14. The distance from point to line.
15. Which of the following statements are true and which are false for all lines and planes in xyz-space: (a) Two lines parallel to a third line are parallel. (b) Two lines perpendicular to a third line are parallel. (c) Two planes parallel to a third plane are parallel. (d) Two planes perpendicular to a third plane are parallel. (e) Two lines parallel to a plane are parallel. (f) Two lines perpendicular to a plane are parallel. (g) Two planes parallel to a line are parallel. (h) Two planes perpendicular to a line are parallel. (i) Two lines are either parallel or intersect. (j) Two planes either are parallel or intersect. (k) A line and a plane either are parallel or intersect. (l) Two non-parallel lines either intersect or there are parallel planes that contain them.
Classroom assignments:
1. Define the distance between points À(3;8) and Â(-5;14).
2. On axe Îõ to find a point with the distance 13 unit from point Ì(2;5).
3. Show that points À(6;3), Â(1;-2), Ñ(-2;-5) belong to one line.
4. The segment bounded by points À(3; -2) and Â(6;4), was divided on three equals parts.
5. Define coordinates of verteces triangle, if it is known the middle its sides Ð(2;3), Q(5;4), R(6;-3).
6. Find polar coordinates of points  ,
, 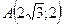 ,
,  ,
,  if the pole coincide with point of origin and polar axe -- with position direction of absciss(a) axe.
if the pole coincide with point of origin and polar axe -- with position direction of absciss(a) axe.
7. Find Rectangular coordinates of points:  .
.
8. Write equation of line passing through the points: à) À(0;2), Â(-3;7); á) À(2;1), Â(4;1).
9. Find angular coefficient to line and ordinate of point its intersection with axe Îó, if it is known line pass through points À(1;1) and Â(-2;3).
10. The coordinates of points Ì1(-3;5) and Ì2(4;6) are given and equation of line d 5x-7y=8=0.
To demand:
1. construct line d and points Ì1 and Ì2;
2. calculate the distance from point Ì1 to line d
3. write equation of line passing through point Ì1, parallel to line d
4. write equation of line passing through point Ì1, perpendicular to line d
5. write equation of line Ì1Ì2;
6. clarify mutual disposition of lines Ì1Ì2 and d;if they are not parallel, to define tangent of angle between them and to find coordinate of points its intersection.
11. Give equations of (a) the line through (5, 6, 7) and parallel to the line x = 4, y = 6 – t, z = 9 + 2t, (b) the line through the origin and perpendicular to the plane 3x – 4y + 5z – 18 = 0
12. What are the numbers a and b if 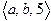 is perpendicular to the plane 4x –2y + z = 5?
is perpendicular to the plane 4x –2y + z = 5?
13. Find the component form of the vector:
a. The vector  where
where  .
.
b. The vector  where O is the origin and
where O is the origin and 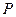 is the midpoint of segment
is the midpoint of segment  , where
, where  .
.
c. The vector from the point  to the origin.
to the origin.
d. The sum of  and
and  , where
, where 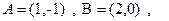

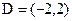 .
.
14. Find a) the direction of 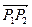 and b) the midpoint of line segment
and b) the midpoint of line segment 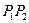 .
.
a. 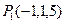 and
and 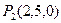
b.  and
and 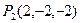
Homework: Function. The limit function. Fundamental theorems on limits. Infinitely small and infinitely large quantities.
Theoretical material: Curves of the second order: circle, ellipse, hyperbola, parabola.
Solve problems:
1. Vertex of triangle ABC are given: 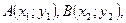
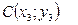 to define coordinates of a point of intersection of medians of a triangle.
to define coordinates of a point of intersection of medians of a triangle.
2. Two vertices of a triangle À(3;8) and Â(10;2) and point of intersection of medians of M (1; 1) are given. Find coordinates of thirds of vertex of a triangle.
3. Make the equation of the line passing through the point of À(-2;1):
à) parallel to the axis Îó;
b) forms an angle 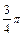 with the Îõ -axis;
with the Îõ -axis;
c) parallel to the bisector of the first quadrantal angle;
d) perpendicular to the straight line 6x-y +2 = 0;
d) cut off on the y-axis segment length of 5.
4. Find the areas of the triangle with vertices P = (2, 1, 0), Q = (3, 4, 5), R = (6, 1, 2).
5. Find the distance from (2, 4 –1) to the plane z = 2x + y + 3. Give parametric equations of the line that passes through the origin and through the intersection of the lines L1: x = 3 + 2t, y = –4t, z = –3 + t and L2: x = 3 + 10t, y = –25 + 5t, z = 4 – 2t.
6. Find the measures of the angles between the diagonals of the rectangle whose vertices are 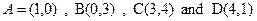
7. Let  . Find the a) component form and b) magnitude (length) of the vector.
. Find the a) component form and b) magnitude (length) of the vector.
a). 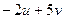 ; b).
; b).  .
.
Date: 2015-01-02; view: 1529