
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Matrix. Operations with matrices. The inverse matrix. Determinants and their properties. Systems of linear equations
Theoretical questions:
1. The concept of matrix;
2. Matrix operations: addition of matrices, multiplication of a matrix by a number, matrix multiplication;
3. Calculating determinants of 2×2 and 3×3 matrices;
4. Solving systems of linear equations matrix method;
5. Solving systems of linear equations on Cramer's rule;
6. Investigation compatible system;
7. Solving systems of linear equations Gauss's method.
Classroom assignments:
1. Matrixes  and
and  are given. Find 3À+2Â.
are given. Find 3À+2Â.
2. Find matrix Õ, if: 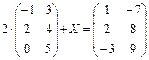
3. Calculate: à)  ;
;
á) ÀÂ, if:  .
.
4. Calculate ÀÂ and ÂÀ, if: 
5. Calculate D= ABC-3E, if: 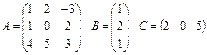
6. Find the values of matrix polynomials:
à)  , åñëè
, åñëè 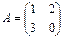
á) 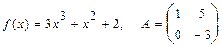
â) 
7. Calculate determinants:

8. Prove that  , if
, if
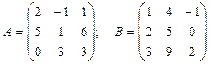
9. Solve systems of linear equations matrix method by matrix method, by Cramer’s formula, investigate systems on compatibility, and solve them by Gauss's method:
a. 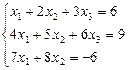 b.
b.  c.
c. 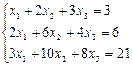
10. Investigate systems on compatibility and, in case of compatibility, solve them by Gauss's method:
a. 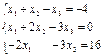 b.
b. 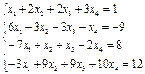 c.
c. 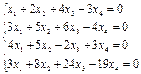
Homework.
Theoretical material: The simplest problem of analytic geometry. Equations of a straight line on a plane. Vectors.
Solve problems:
1.Calculate 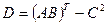 , if:
, if: 
2.Find ÀÂÑ, if: 
3.Prove, that 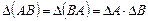 , if:
, if: 

4.Solve systems of linear equations matrix method by matrix method and by Cramer’s formula:
a.  b.
b. 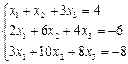
5. Investigate systems on compatibility and, in case of compatibility, solve them by Gauss's method: 
Date: 2015-01-02; view: 1629
| <== previous page | | | next page ==> |
| Trigonometric form of a complex number, de Moivre's formula | | | PRACTICAL CLASS ¹ 3-5. |