
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
COMPLEX NUMBER. COMPLEX NUMBERS IN TRIGONOMETRIC AND EXPONENTIAL FORM
LECTURE PLAN:
1. Complex numbers
2. Complex numbers in trigonometric and exponential form
Complex numbers
The main theorem of algebra. An algebraic equation of the nth degree
xn+an-1xn-1+…+a1x+a0=0
has n zeros. (Without a proof.)
Example.
x3-1=0, (x-1)(x2+x+1)=0, x1=1,
x2+x+1=0; D=1-4=-3,
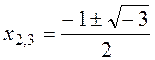 - not real numbers.
- not real numbers.
Definition. The number 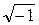 is called the imaginary unit and is denoted by
is called the imaginary unit and is denoted by 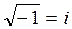
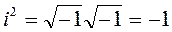 ; i3=-i;
; i3=-i;
i4=i2.i2=(-1).(-1)=1; i5=i;
i6=-i and so on. i.e. is a multiple of 4.
Example. Find
i35= i32+3 =i3=-i.
Definition. A number of the form a=a+bi is called a complex number, where, i is the imaginary unit and à, b are real numbers. Numbers à and bi are called the real and the imaginary parts of a complex number.
The following is a geometric interpretation of a complex number
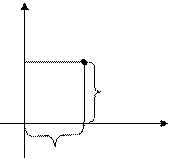 |
ó
Ì(a,b)
a=a+bi
b
0 x
a
Each complex number corresponds to a point of the coordinate plane õOó. Each real number is also a complex number with zero imaginary part, i.e. b=0. For example, 32=32+0i.
Operations on complex numbers
1) Addition of complex numbers.
Consider complex numbers a1 =a1 +b1i, a2 =a2 +b2i.
Add them and combine the like terms
a1 +a2 =a1 +b1i +a2 +b2i= (a1 +a2) +i(b1+b2),
We add separately the real and the imaginary parts.
2) Subtraction a1–a2 = (a1–a2) +i(b1–b2).
Geometrically, addition and subtraction of complex numbers is performed exactly in the same way as addition and subtraction of the vectors with corresponding coordinates.
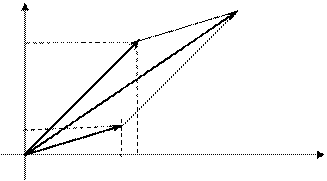 y
y
 a1+a2
a1+a2
b2 a2
a1-a2
b1
a1
0 a1 a2 x
3) Multiplication.
a1 . a2 =(a1 +b1i)(a2 +b2i)= a1a2+b2ia1+b1a2i+b1b2i2=
=(a1a2-b1b2)+i( a1b2 +b1a2), ò.ê. i2=-1.
Multiplication of complex numbers is performed as usual multiplication of algebraic expressions; after the multiplication the real and imaginary parts are grouped separately.
The numbers a =a +bi, a =a –bi are called complex conjugates or simply conjugates.
The product of two conjugates is a nonnegative real number a2+bia-abi-i2b2=a2+b2.
4) Division. Definition. The quotient 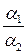 of two complex numbers is a
of two complex numbers is a
complex number b such that  .
.
Suppose,  , then by the definition
, then by the definition
 ;
;
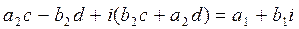 .
.
Due to equality of real and imaginary parts,
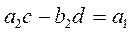 ;
;  .
.
Solve the resulting system of linear equations
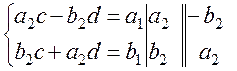 ,
,
and find the real numbers c and d
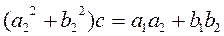 ,
,
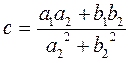 ,
, 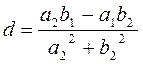 .
.
The denominator of both expressions is the product of two conjugates,
so let us multiply both the numerator and the denominator of 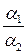 by the conjugate of the denominator
by the conjugate of the denominator
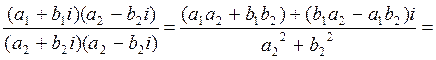
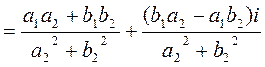 - as expected, the result equals b.
- as expected, the result equals b.
Rule. In order to find the quotient of two complex numbers, it is enough to multiply both the numerator and the denominator by the conjugate of the denominator, and then separate the real and imaginary parts.
Examples. 1. Divide
 .
.
2. Solve the equation õ2-2õ+10=0 and check Viete's theorem for the complex zeros
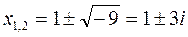 ;
;
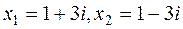 ; x1+x2=2; x1 .x2=12+32=10.
; x1+x2=2; x1 .x2=12+32=10.
The magnitude and argument of a complex number. Plot the complex number a=a+bi on the  plane.
plane.
 ó
ó
r b
j
0 a x
It is easy to see that r2=a2+b2 and  ; the numbers ρ and j are called the absolute value (or magnitude) and the argument of a complex number respectively.
; the numbers ρ and j are called the absolute value (or magnitude) and the argument of a complex number respectively.
Date: 2015-01-02; view: 1744