
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
LECTURE 8
Investigation of the function. Extremum of the function. Necessary and sufficient conditions for the existence of an extremum. Convexity, concavity and inflection points. Asymptote. The overall study of design features
1. Monotonic conditions. Extremum of function
2. Convexity and concavity. Point of inflection
3. Àsymptotes
4. General Scheme for the Investigation of the Graph of a Function
Monotonic conditions. Extremum of function
Theorem 1. Let  be continuous on [a, b] and differentiable on (a, b).
be continuous on [a, b] and differentiable on (a, b).  is a constant
is a constant
function if and only if  for all
for all  .
.
Definition 1. A function  is said to be monotonic increasing (resp. monotonic decreasing )
is said to be monotonic increasing (resp. monotonic decreasing )
or simply increasing ( resp. decreasing ) on an interval  if and only if
if and only if 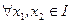 , if
, if 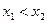
then 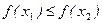 (resp.
(resp. 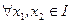 , if
, if 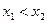 , then
, then 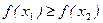 ).
).
Definition 2. A function  is said to be strictly increasing ( resp. strictly decreasing ) on an
is said to be strictly increasing ( resp. strictly decreasing ) on an
interval  if and only if
if and only if 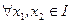 , if
, if 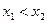 then
then 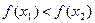 (resp.
(resp. 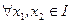 , if
, if 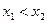 ,
,
then 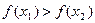 ).
).
Theorem 2. Let  be continuous on [a, b] and differentiable on (a, b). Then
be continuous on [a, b] and differentiable on (a, b). Then
(a) if 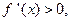

 is strictly increasing on [a, b]; and
is strictly increasing on [a, b]; and
(b)if 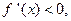

 is strictly decreasing on [a, b].
is strictly decreasing on [a, b].
Definition 3. A neighborhood of a point  is an open interval containing
is an open interval containing  , i.e.
, i.e.  is a neighborhood of
is a neighborhood of  for some
for some  .
.
Definition 4. A function  is said to attain a relative maximum (minimum ) at a point
is said to attain a relative maximum (minimum ) at a point  if
if
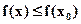 (
(  ) in a certain neighborhood of
) in a certain neighborhood of  , i.e.
, i.e.  such that
such that 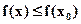 (
(  ) for
) for 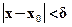 .
.
Theorem (Fermat Theorem).
Given  is a point defined on
is a point defined on  and differentiable at a point
and differentiable at a point 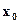 if
if  has an extreme value ( max. or min )
has an extreme value ( max. or min )  , then
, then  .
.
 Note
Note 

 has maximum or minimum at
has maximum or minimum at  .
.
Definition 5. (a) A turning point is a maximum or minimum point.
(b) If 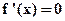 , then
, then 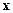 is called a critical or
is called a critical or
stationary value and its corresponding point on the graph 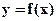 is called stationary point.
is called stationary point.
Notes
1. turning point stationary point
2. turning point + differentiable  stationary point
stationary point
3. stationary point turning point
Convexity and concavity. Point of inflection
Let 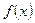 be a function differentiable on an interval J. The function f is called convex (concave) on J, if all points of its graph on J lie above (below) any tangent line to
be a function differentiable on an interval J. The function f is called convex (concave) on J, if all points of its graph on J lie above (below) any tangent line to 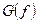 on this interval (excepting point of tangency). Let f be continuous at a point
on this interval (excepting point of tangency). Let f be continuous at a point 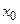 . If there exists
. If there exists  such that f is concave (convex) in
such that f is concave (convex) in 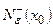 and convex (concave) in
and convex (concave) in 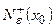 , the point
, the point 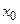 is called the point of inflection of
is called the point of inflection of 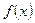 .
.
The second Derivative Test for Concavity and Convexity:
If  , for each
, for each  , then
, then 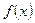 is convex on J,
is convex on J,
if 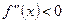 , for each
, for each  , then
, then 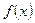 is concave on J.
is concave on J.
It follows:
If 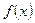 is continuous at
is continuous at 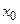 and
and  (
( 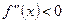 ) in
) in 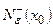 and
and 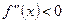 (
(  ) in
) in 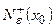 , then
, then 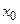 is a point of inflection.
is a point of inflection.
Moreover: If 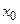 is a point of inflection of f, then either
is a point of inflection of f, then either  or
or  doesn’t exist.
doesn’t exist.
If f is three times differentiable at a point 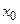 ,
,  and
and 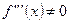 , then
, then 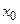 is a point of inflection.
is a point of inflection.
Definition 6. Given that  is continuous on
is continuous on 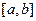 , if any
, if any  such that
such that
 (i)
(i)  (ii)
(ii) 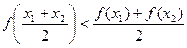
 Concave Downward Concave Upward
Concave Downward Concave Upward
Theorem 3. If  is a function on
is a function on 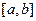 such that
such that  is second differentiable on
is second differentiable on  then
then
(i)  iff
iff  is concave upward on
is concave upward on 
(ii) 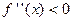 iff
iff  is concave downward on
is concave downward on  .
.
Definition 7. Let  be a continuous function. A point
be a continuous function. A point 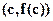 on the graph of
on the graph of  is a point of inflexion (point of inflection) if the graph on one side of this point is concave downward and concave upward on the other side. That is, the graph changes concavity at
is a point of inflexion (point of inflection) if the graph on one side of this point is concave downward and concave upward on the other side. That is, the graph changes concavity at  .
.

Note A point of inflexion of a curve 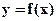 must be a continuous point but need not be differentiable there. In Figure (c), R is a point of inflexion of the curve but the function is not differentiable at
must be a continuous point but need not be differentiable there. In Figure (c), R is a point of inflexion of the curve but the function is not differentiable at 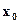 .
.
Theorem 4. If  is second differentiable function and attains a point of inflexion at
is second differentiable function and attains a point of inflexion at  , then
, then
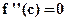 .
.
Note:
(i) max. or min. point but not derivative.
(ii) point of inflexion may not be obtained by solving 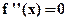 where
where  and
and 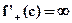 such that
such that  .
.
(iii) Let  be a function which is second differentiable in a neighborhood of a point of inflexion iff
be a function which is second differentiable in a neighborhood of a point of inflexion iff 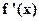 does not change sign as
does not change sign as 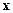 increases through (sign gradient test)
increases through (sign gradient test)
– if 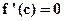 and
and  , then
, then  attains a relative max. or relative min.
attains a relative max. or relative min.
– if 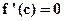 and
and  , then
, then  attains an inflexion point at
attains an inflexion point at  .
.
Asymptotes
If a function f gets close to a certain number L when x gets larger and larger, then we say that the limit as x goes to infinity is L and we write:  . Likewise, if f gets close to L when x gets smaller and smaller, then the limit as x goes to negative infinity is L and we write:
. Likewise, if f gets close to L when x gets smaller and smaller, then the limit as x goes to negative infinity is L and we write:  . In both cases, the line y = L is a horizontal asymptote of f.
. In both cases, the line y = L is a horizontal asymptote of f.
 Example:
Example: 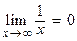 because when x is very large,
because when x is very large, 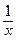 is close to 0. The x-axis is a horizontal asymptote of the function
is close to 0. The x-axis is a horizontal asymptote of the function 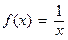 :
:
If a function 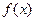 gets larger and larger as x gets close to a number a, then it “goes to infinity” and we write:
gets larger and larger as x gets close to a number a, then it “goes to infinity” and we write:  . The line x = a is a vertical asymptote of f. Similarly, if
. The line x = a is a vertical asymptote of f. Similarly, if 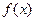 gets smaller and smaller as x gets close to a, then it “goes to negative infinity” and we write:
gets smaller and smaller as x gets close to a, then it “goes to negative infinity” and we write:  . Again, the line x = a is a vertical asymptote of f.
. Again, the line x = a is a vertical asymptote of f.
An important result:
If  then
then 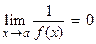 . This is because one over a very large positive number and one over a huge negative number are both close to 0.
. This is because one over a very large positive number and one over a huge negative number are both close to 0.
Inclined asymptotes have an equation y = kx + q and their position is arbitrary except vertical. In order a straight line y = kx + q be an asymptote, the coefficients k and q must satisfy at least one pair of the following conditions
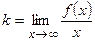 and
and 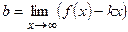 (k and b are numbers).
(k and b are numbers).
Naturally these limits must be finite real numbers. A certain function can have maximally two inclined asymptotes.
General Scheme for the Investigation
of the Graph of a Function
The following information is useful for sketching the graph of 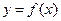
(1) The domain of  , i.e. the range of values of
, i.e. the range of values of 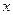 within which
within which  is well-defined.
is well-defined.
(2) Determine whether  is periodic, odd or even, so that the graph may be symmetric about the coordinate axes or about the origin.
is periodic, odd or even, so that the graph may be symmetric about the coordinate axes or about the origin.
(3) Turning points and monotonicity of  .
.
(4) Inflectional points and convexity of  .
.
(5) Asymptotes including horizontal, vertical and oblique ones (if any).
(6) Some special points on the graph, such as intercepts.
Date: 2015-01-02; view: 1698