Rolle's theorem, Lagrange, Cauchy. L'Hopital's rule

LECTURE PLAN:

1. Properties of differentiable functions

2. Limits- indeterminate forms and L’Hospital’s Rule

Properties of differentiable functions

Fermat's Theorem.

Let be defined and differentiable on an open interval (a, b). If attains its absolute maximum or absolute minimum (both are called absolute extremum) at 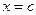, where 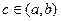, then .

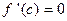Rolle's Theorem.

If a function satisfies all the following three conditions:

(1) is continuous on the closed interval ,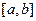

(2) is differentiable in the open interval ,

(3) ;

then there exists at least a point 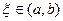such that .

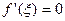Lagrange's Theorem.

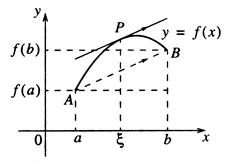If a function is

(1) continuous on the closed interval 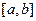and

(2) differentiable in the open interval ,

then there exists at least a point 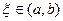such that

.

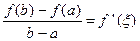Limits- indeterminate forms and L’Hospital’s Rule

I. Indeterminate Form of the Type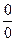

We have previously studied limits with the indeterminate form 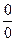as shown in the following examples:

Example 5: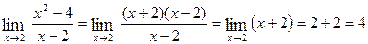

However, there is a general, systematic method for determining limits with the indeterminate form 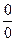. Suppose that f and g are differentiable functions at x = a and that is an indeterminate form of the type 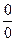; that is, and . Since f and g are differentiable functions at x = a, then f and g are continuous at x = a; that is, 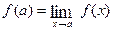= 0 and 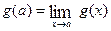= 0. Furthermore, since f and g are differentiable functions at x = a, then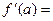 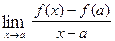and 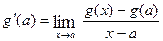. Thus, if 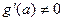, then

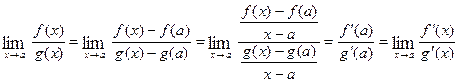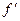if and

are continuous at x = a. This illustrates a special case of the technique known as

L’Hospital’s Rule.

The Bernoulli-L'Hopital Rule

This rule is used for finding the ratio limits of the form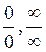

Theorem 1. Suppose that there are differentiable functions f(x) and j(x) on the interval [a;b] and f(a)=j(a)=0, then having limit 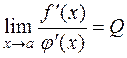, there is the limit which equals

.

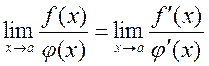In the following examples, we will use the following three-step process:

Step 1. Check that the limit of 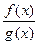is an indeterminate form of type 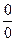. If it is not, then L’Hospital’s Rule cannot be used.

Step 2. Differentiate f and g separately. [Note: Do not differentiate 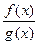using the quotient rule!]

Step 3. Find the limit of . If this limit is finite, 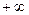, or 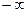, then it is equal to the limit of 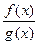. If the limit is an indeterminate form of type 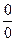, then simplify algebraically and apply L’Hospital’s Rule again.

Example 6:

II. Indeterminate Form of the Type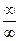

We have previously studied limits with the indeterminate form 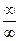as shown in the following examples:

Example 7:

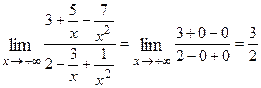
However, we could use another version of L’Hospital’s Rule.

L’Hospital’s Rule for Form

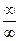
Suppose that f and g are differentiable functions on an open interval

containing x = a, except possibly at x = a, and that and

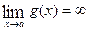. If 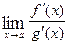has a finite limit, or if this limit is 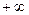or

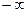, then 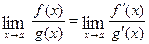. Moreover, this statement is also true

in the case of a limit 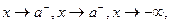as or as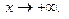

III. Indeterminate Form of the Type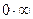

Indeterminate forms of the type 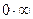can sometimes be evaluated by rewriting the product as a quotient, and then applying L’Hospital’s Rule for the indeterminate

forms of type 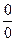or .

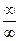Example 8: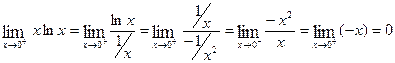

IV. Indeterminate Form of the Type

A limit problem that leads to one of the expressions

, , ,

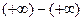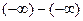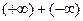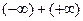
is called an indeterminate form of type . Such limits are indeterminate because the two terms exert conflicting influences on the expression; one pushes it in the positive direction and the other pushes it in the negative direction. However, limits problems that lead to one the expressions

, , ,

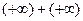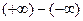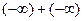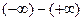
are not indeterminate, since the two terms work together (the first two produce a limit of 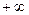and the last two produce a limit of 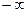). Indeterminate forms of the type can sometimes be evaluated by combining the terms and manipulating the result to produce an indeterminate form of type 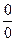or .

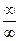Example 9: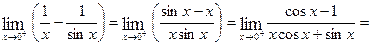

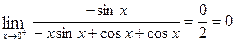
V. Indeterminate Forms of the Types

Limits of the form 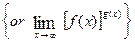frequently give rise to indeterminate forms of the types . These indeterminate forms can sometimes be evaluated as follows:

(1)

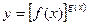
(2)

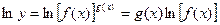
(3)

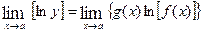
The limit on the righthand side of the equation will usually be an indeterminate limit of the type 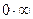. Evaluate this limit using the technique previously described. Assume that 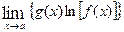= L.

(4) Finally, .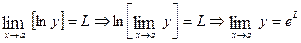

Example 10: Find .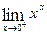

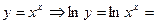
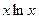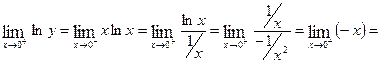This is an indeterminate form of the type . Let . 0.

Thus, .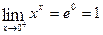

Taylor’s formula

Suppose we’re working with a function f(x) that is continuous and has n+1 continuous derivatives on an interval about x = 0. We can approximate f near 0 by a polynomial 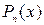of degree n:

• For n = 0, the best constant approximation near 0 is 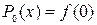which matches f at 0.

• For n = 1, the best linear approximation near 0 is 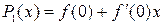. Note that 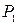matches f at 0 and 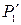matches 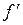at 0.

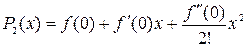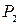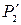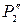• For n = 2, the best quadratic approximation near 0 is . Note that , , and match , , 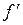and 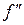, respectively, at 0.

Continuing this process,

.

This is the Taylor polynomial of degree n about 0 (also called the Maclaurin series of degree n). More generally, if f has n+1 continuous derivatives at x = a, the Taylor series of degree n about a is

.

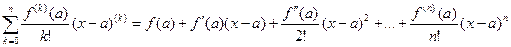This formula approximates f (x) near a. Taylor’s Theorem gives bounds for the error in this approximation:

Taylor’s Theorem:

Suppose f has n+1 continuous derivatives on an open interval containing a. Then for each x in the interval,

,

where the error term 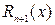satisfies 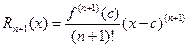for some c between a and x.

This form for the error 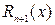, derived in 1797 by Joseph Lagrange, is called the Lagrange formula for the remainder. The infinite Taylor series converges to f ,

,

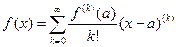if and only if .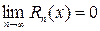

Date: 2015-01-02; view: 2077