Carry out a system design procedure using observer design method

The tasks for the Term Paper (Control systems).

1. Obtain the system transfer functions:

- for control input signal (x/Td=0);

- for disturbance input signal (Td/x=0);

using block diagram transformation theorems;

2. Obtain the system transfer functions:

using the Mason’s gain rule and compare the obtained results with the results in item.1;

- for control input signal (x/Td=0);

- for disturbance input signal (Td/x=0);

3. Obtain your system’s state-space models:

- for control input signal (x/Td=0);

- for disturbance input signal (Td/x=0);

4. Compare the characteristics (step response, impulse response, Nyquist diagram, Bode diagram, Nichols diagram, Gain and Phase Margins, Pole/Zero Map) of your control system equivalent transfer functions for control input signal (x/Td=0) and disturbance input signal (Td/x=0) (obtained by the usage of block diagram transformation theorems and the Mason’s gain rule) using the possibilities of linear analysis.

5. Carry out a system design procedure using various methods and define the best controller characteristics:

5.1. Carry out a system design procedure using the root locus method.

- gain margin: 10 dB<GM<40 dB;

- phase margin 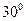<PM< ;

5.2. Carry out a system design procedure using the phase lead regulator method.

- gain margin: 10 dB<GM<40 dB;

- phase margin 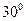<PM< ;

5.3. Carry out a system design procedure using the phase lag regulator method.

- gain margin: 10 dB<GM<40 dB;

- phase margin 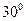<PM< ;

5.4. Carry out a system design procedure using the PID regulator method.

- gain margin: 10 dB<GM<40 dB;

- phase margin 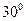<PM< ;

Carry out a system design procedure using pole placement method

FIGURE 1 Block diagram of a closed-loop control system.

Carry out a system design procedure using observer design method

- for control input signal (x/Td=0);

- for disturbance input signal (Td/x=0);

8. Define the static characteristics of your system with a controller:

- for control input signal (x/Td=0);

- for disturbance input signal (Td/x=0);

9. Obtain position, velocity and acceleration errors in steady-state mode for the control system with a controller;

- for control input signal (x/Td=0);

- for disturbance input signal (Td/x=0);

10. Research sensitivity parameters of your control system with a controller;

- for control input signal (x/Td=0);

- for disturbance input signal (Td/x=0);

11. Define controllability and observability of the control system with a controller.

12. Define the ways to reduce the influence of the band-limited white noise on the characteristics of the control system with a regulator;

FIGURE 1 Block diagram of a closed-loop control system ( = a controller, = a plant, = feedback control loop).

13. Define the ways to reduce the influence of a nonlinear element (dead zone) on the characteristics of your control system

FIGURE 2 Block diagram of a closed-loop control system ( = a controller, = a plant,NLE– nonlinear element (dead zone), = feedback control loop).

Date: 2015-12-24; view: 1184