
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Tangents to an Ellipse
Consider the equation of an ellipse:
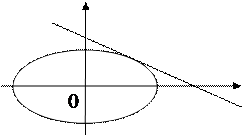 ó
ó 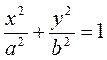 .
.
Ì0(õ0;ó0)
õ
As is known, the equation of a tangent to a curve is determined by the formula
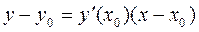 .
.
Differentiating the equation of the ellipse as an implicit function, we obtain 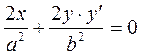 , whence
, whence 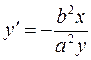 , or
, or 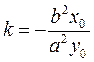 .
.
Substituting this k, we find the equation of the tangent line:
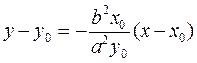 .
.
Let us transform it:
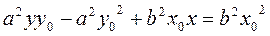 ,
,
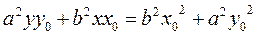 . Dividing by
. Dividing by 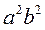 , we obtain
, we obtain
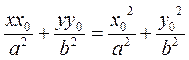 .
.
Since the point Ì0 belongs to the ellipse, the coordinates of Ì0 must satisfy its equation, and the right-hand side equals one.
Thus, the equation of a tangent to an ellipse is
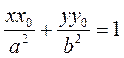 . (18)
. (18)
Example. Given the ellipse given 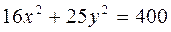 , find the distance between its foci, eccentricity, and the equations of directrices.
, find the distance between its foci, eccentricity, and the equations of directrices.
Let us reduce the equation it to the classical form (17):
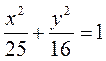 ;
; 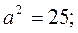
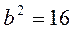 ;
;
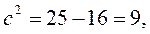
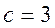 ,
, 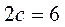 .
.
Let us find the eccentricity:
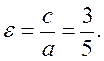
The equations of the directrices are
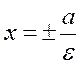 ,
, 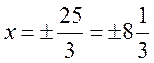 .
.
Hyperbola
Definition. The locus of the points for which the difference of distances to two fixed points is constant equal to 2à is called a hyperbola.
As for an ellipse, we introduce a new coordinate system:
 |

 ó
ó
 |
Ì(õ,ó)

 r1 r2
r1 r2

F1(–c,0) M1 M2 F2(c,0) x
To derive the equation of a hyperbola, we take an arbitrary point Ì(õ,ó) on the hyperbola and consider the distances from this point to the foci:
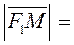
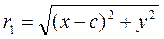 ;
; 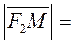
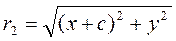 .
.
The characteristic feature of the line is, by definition,
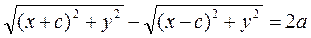 .
.
We have composed an equation of the hyperbola. Let us reduce to a convenient form (by analogy with the ellipse):
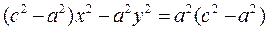 .
.
We divide both sides by 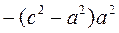 :
:
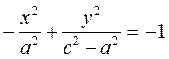
Changing the sign, we obtain the equation of a hyperbola:
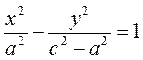 .
.
Since 2a<2c, we denote the difference of squares by
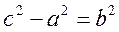 . (**)
. (**)
Thus, we have obtained the classical equation of a hyperbola:
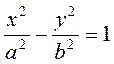 . (19)
. (19)
Date: 2015-01-02; view: 1543
| <== previous page | | | next page ==> |
| The eccentricity and directrix of an ellipse. Consider the focal radii of an ellipse | | | Asymptotes of a Hyperbola |