
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Triple Product in Coordinates. Given three vectors , , and , let us express the triple product of these vectors in terms of their coordinates. Consider the triple product
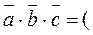

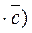 .
.
The vector product equals
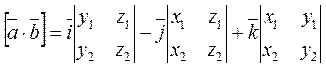 .
.
Taking its inner product with 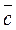 , we obtain
, we obtain
 ;
;
this is a third – order determinant expanded along the last line, i.e.,
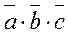
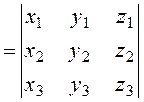 .
.
Thus, the triple product of three vectors equals the third – order determinant of the composed of the coordinates of these vectors.
Example 1. Determine the volume of a pyramid ABCD from the coordinates of its vertices.
   D(1;5;2)
B(–1;1;3)
A(1;2;0)
C(0;2;–3) D(1;5;2)
B(–1;1;3)
A(1;2;0)
C(0;2;–3)
| Compose the vectors
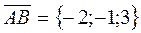 , ,
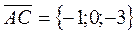 , ,
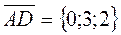 . .
|
Let us find the volume of a pyramid by the formulas proved above:
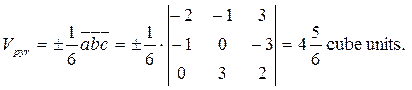
The triple product of coplanar vectors equals zero.
The triple product equals
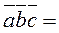
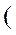
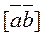
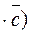
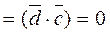 , because
, because 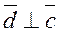 .
.
Thus, the coplanarity condition is
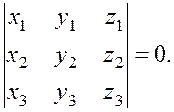
Example 2. Show that the four points À(1;2;–1), Â(0;1;5), Ñ(–1;2;1), and D(2;1;3) belong to the same plane.
 B
C
A
D B
C
A
D
| Compose the vectors
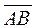 ={–1;–1;6}, ={–1;–1;6},
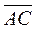 ={–2;0;2}, ={–2;0;2},
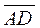 ={1;–1;4}. ={1;–1;4}.
|
To show that they are coplanar, we find the triple product
 .
.
Thus, the four points belong to the same plane.
Date: 2015-01-02; view: 3147
| <== previous page | | | next page ==> |
| Consider vectors | | | Ellipse |