
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Consider vectors
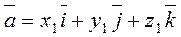 and
and 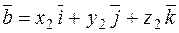 .
.
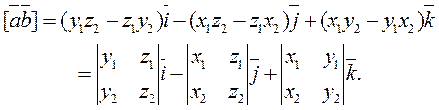
Note that the right – hand side is the expansion of a third – order determinant along the row with elements  and
and  .
.
Thus, the coordinates of the vector product are determined form the third – order determinant as
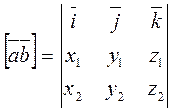 , (9)
, (9)
and its absolute value is
 .
.
Example 1. Given the vectors 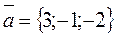 and
and  , find the vector products (à)
, find the vector products (à) 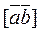 ; (b)
; (b) 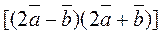
(à) Let us use the expression (9) a vector product:

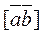
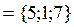 .
.
(b) Let us find the required product by using associativity:

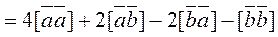
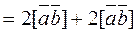 =
=  ,
,
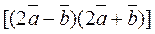 =
= 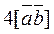 .
.
Since the second product is expressed linearly in terms of the first, it sufficed to multiply the coordinates of the first vector by 4: 
 , whence
, whence 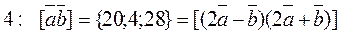 .
. 
Triple Product of Vectors and its Properties
Definition. The triple product of three vectors is the inner product of the third vector by the vector product of the first two vectors; it is denoted by

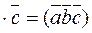 .
.
Definition. The vector product of the vector product of the first two vectors and the third vector ones is called the double vector product:

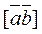
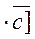 .
.
Since double vector product is used very rarely, it have been little studied.
Property 1. The triple product of three vectors equals the volume of a parallelepiped spanned by these three vectors.
Corollary. It is easy to derive an expression for the volume of a pyramid from the formula:
S
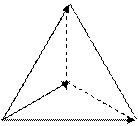 |

B
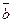
À Ñ
Vðyr=  Sbase Í =
Sbase Í = 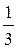 .
. 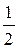 Sðar Í =
Sðar Í = 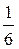 Vðar=
Vðar= 
 ,
,
Vðyr= 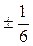
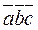 .
.
The sign  is needed to obtain a positive volume.
is needed to obtain a positive volume.
Property 2. Triple product is commutative, and
 .
.
Property 3. A constant multiplier of any vector can be factored out of scalar triple product:
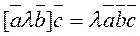 .
.
Date: 2015-01-02; view: 1604