
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Lesson 8: Distance Lesson Plan
| Lesson Component | Description of Component For This Lesson |
| Lesson Opening (10 minutes) Introduction of New Material (15 - 20 minutes) | Objective: To compute distances in a coordinate plane. SWBAT:
(1) Plot points and connect them with line segments
(2) Given two points in a coordinate plane compute the distance between them/the length of the line segment connecting them using the distance formula.
Use a “Do Now” to review square roots:
(1) Mini-lesson
I will plot an example on graph chart paper that shows a right triangle using the x and y axis and starting at the origin to show that from the origin to a point the Pythagorean Theorem may be used.
distance from  to to  is is  I will then show that a right triangle may be drawn with a point other than the origin as one of the vertices and use the complete distance formula. Distance from
I will then show that a right triangle may be drawn with a point other than the origin as one of the vertices and use the complete distance formula. Distance from  to to  is is
 (2) Engagement
I will talk about how many times in the city, we can’t use a straight line because of buildings in the way but when we can cut across it cuts down on the distance we have to travel.
(2) Engagement
I will talk about how many times in the city, we can’t use a straight line because of buildings in the way but when we can cut across it cuts down on the distance we have to travel.
|
| Student Practice of New Material (30 minutes) | (9) Exploration/Application Students will graph various points and determine how far away they are from the origin. Students will then progress to determining the distance between points in the first quadrant. I will introduce a challenge question that requires finding the distance between points in different quadrants. (4) Assessment The assessment will be ongoing as I walk around the room while students plot their points and determine distance. As part of the assessment, I will have the students complete a quick exit ticket to be handed in at the end of class. |
| Summary (5 minutes) | I will summarize the formula for distance and remind students that we are using the Pythagorean Theorem to find the hypotenuse. |
| Exit Ticket | Hand out graph paper sheet. Students plot pairs of points and use the distance formula to determine how far apart the two points are. 1. (0, 0) and (-3, -4) 2. (-4, -6) and (1, 6) |
Homework
Fill in the table using the Pythagorean Theorem

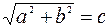
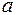
| 
| 
| 
| 
|  to 4 decimals to 4 decimals
| 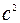
|

| ||||||

|

|
|
|
Graph the triangle (0,0), (4,0), (4,3). What is the distance from (0,0) to (4,3)?
|

Graph the triangle:
(-3,0), (2,0), (2,6). What is the distance from (-3,0) to (2,6)?
Date: 2015-12-24; view: 952
| <== previous page | | | next page ==> |
| Lesson 6: Perfect Squares and Irrational Number | | | Lesson 9: Proportion and Scale |