Lesson Opening(10 minutes)Introduction of New Material(5 minutes)
Objective: To compute square roots and compare number systems. SWBAT: (1) compute square roots using a calculator or approximations for both perfect squares and non-perfect squares(2) identify a number as rational or irrational(3) graph and put numbers in correct sequential orderI will use a “Do Now” to continue a review of simplifying polynomial expressions: 5xy2 + 2x – (2xy2 – x) 4y3z + 4y2 + 2y2 + 3y3z(1) Mini-lessonI will briefly discuss rational and irrational numbers and look at how to bracket a square root between two perfect squares. I will use a concept map to explain the table that students will fill out during exploration.(2) EngagementI will hand out graph paper and have students create squares with various side lengths and have them count or multiply to determine the number of square units of area for each perfect square.
Student Practice of New Material
(20 minutes)
Exploration/Application
Students will first complete a table that reinforces the concept of “squaring” and “square root” as inverses.
Students will then fill out a work sheet with perfect squares and non-perfect squares and look at the “square root” as the opposite of “squaring”. They will first bracket the square root and make an a guess as to the value of the square root. They will then take calculators and determine the square roots to 4 decimal places.
Summary
(5 minutes)
(4) Assessment
The assessment will be ongoing as I walk around the room while students fill out work sheets. I will do a quick summary of perfect squares.
a
1. 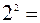2. 3. 4.
5. 6. 7. 8.
9. 10. 11.
Fill out the below table by finding the two integers that bracket the square root. Estimate the square root to one decimal place. Use a calculator to check your estimate and write down the square root to 4 decimal places. Follow the example.
Integer <
< Integer
Estimate
Calculator Value
2.2
2.2361
Lesson Component
Description of Component For This Lesson
Lesson Opening
(10 minutes)
Introduction of New Material
(15 - 20 minutes)
Objective: To compute the length of the hypotenuse of a right triangle using the Pythagorean Theorem. SWBAT:
(1) Identify the legs and hypotenuse of a right triangle
(2) Given the lengths of two of the legs of a right triangle, compute the length of the third side.
I will use a “Do Now” to review the area of a triangle.
Area =
I plan to use right triangles in the Do Now to keep it simple
(1) Mini-lesson
What is the Pythagorean Theorem?
A relationship among the sides of a triangle. I will show an example using 3, 4, and 5.
I will use a flow chart to relate the ideas in the theorem.
(2) Engagement
I will use a sheet of graph paper for each student to demonstrate a proof of the theorem.
Student Practice of New Material
(35-40 minutes)
(8) Exploration/Application
I will use an example to get students interested. A wall is supported by a brace 10 feet long, as shown in the diagram below. If one end of the brace is placed 6 feet from the base of the wall, how many feet up the wall does the brace reach?
I will use a work sheet for practice and another for homework.
(4) Assessment
The assessment will be ongoing as I walk around the room observing students.
Summary
(5 minutes)
I will restate the Pythagorean Theorem and restate that we can solve for any side of the triangle as long as it is a right triangle.
2. 
3. 
4. 
6. 
7. 
8. 
10. 
11. 
I plan to use right triangles in the Do Now to keep it simple
(1) Mini-lesson
What is the Pythagorean Theorem? 
A relationship among the sides of a triangle. I will show an example using 3, 4, and 5.
I will use a flow chart to relate the ideas in the theorem.
(2) Engagement
I will use a sheet of graph paper for each student to demonstrate a proof of the theorem.
I will use a work sheet for practice and another for homework.
(4) Assessment
The assessment will be ongoing as I walk around the room observing students.