
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
is obtained by substituting the second column of free terms.
179.If the determinant of the system is different from zero, then the solution of the system: 
182.Solution of the system  are:
are:
x1=1, x2=-2.
x1=-1, x2=2.
190.A square matrix A n-th order is called degenerate if: detA=0
1.Solve the system if equations: 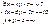 !!!!!! (-4; 2; -1).
2.The point of intersection of the circumference (õ-4)2+ó2=25: !!!!!! Ì(0; !!!!!! (-4; 2; -1).
2.The point of intersection of the circumference (õ-4)2+ó2=25: !!!!!! Ì(0;  3)
3.Show the equation of circumference, where the center is situated in point (2;-3) and circumference passes through the point (5;1): !!!!!!!!!!! (õ-2)2+(ó+3)2=25.
4.The distance between centers of the circumferences õ2+ó2=16 and (õ+3)2+(ó+4)2=25: !!!!! 5
18.Abscissa of the circumference’s point õ2+(ó+4)2=41 and the point on it with ordinate equals zero: !!!!!! 5
19.The curve, specified by equalization (õ-à)2+(ó-b)2=r2: !!!!!!! Circumference.
20.Ordinate of the circumference’s point (õ+3)2+ó2=25, where abscissa equals zero: !!!!! 4
21. A canonical equalization of the ellipse: !!!! 3)
3.Show the equation of circumference, where the center is situated in point (2;-3) and circumference passes through the point (5;1): !!!!!!!!!!! (õ-2)2+(ó+3)2=25.
4.The distance between centers of the circumferences õ2+ó2=16 and (õ+3)2+(ó+4)2=25: !!!!! 5
18.Abscissa of the circumference’s point õ2+(ó+4)2=41 and the point on it with ordinate equals zero: !!!!!! 5
19.The curve, specified by equalization (õ-à)2+(ó-b)2=r2: !!!!!!! Circumference.
20.Ordinate of the circumference’s point (õ+3)2+ó2=25, where abscissa equals zero: !!!!! 4
21. A canonical equalization of the ellipse: !!!! 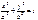 22.The curve, set by the equalization
22.The curve, set by the equalization 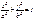 : !!!!!!!!!!! Ellipse.
23.The point of intersection the hyperbola õ2-4ó2=16 with the axis of abscissas: !!! Ì( ±4; 0).
27.Equalizations of asymptotes of the hyperbola : !!!!!!!!!!! Ellipse.
23.The point of intersection the hyperbola õ2-4ó2=16 with the axis of abscissas: !!! Ì( ±4; 0).
27.Equalizations of asymptotes of the hyperbola 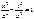 : !!!!! : !!!!! 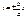 28.Equalizations of asymptotes of the hyperbola
28.Equalizations of asymptotes of the hyperbola  : !!!! : !!!! 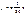 .
29.Describe the distance d from origin coordinates to point Ì(õ;ó): !!!!! .
29.Describe the distance d from origin coordinates to point Ì(õ;ó): !!!!! 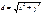 ;
33.Length of the cutoff ÀÂ with the coordinates À(õ1;ó1) and Â(õ2;ó2): ;
33.Length of the cutoff ÀÂ with the coordinates À(õ1;ó1) and Â(õ2;ó2):  36.Coordinates of the interval’s midpoint ÀÂ, À(õ1;ó1)and Â(õ2;ó2):
36.Coordinates of the interval’s midpoint ÀÂ, À(õ1;ó1)and Â(õ2;ó2):  .
39.A rectangle prescribed by coordinates of its apices À(1; 1), Â(8;-5), Ñ(3;5).Point Ì the midpoint of the leg ÀÑ. Length of the median ÂÌ equals: !!!!!! 10
40.Disposition of straight Àõ+Âó+Ñ=0, if Â=0, Ñ .
39.A rectangle prescribed by coordinates of its apices À(1; 1), Â(8;-5), Ñ(3;5).Point Ì the midpoint of the leg ÀÑ. Length of the median ÂÌ equals: !!!!!! 10
40.Disposition of straight Àõ+Âó+Ñ=0, if Â=0, Ñ 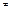 0: !!!!!! parallel to axis ÎÕ
41. Angular coefficient of the straight 2,5ó-5õ+5=0: !!!! 2
42.Disposition of stright Àõ+Âó+Ñ=0, åñëè À=0, Ñ 0: !!!!!! parallel to axis ÎÕ
41. Angular coefficient of the straight 2,5ó-5õ+5=0: !!!! 2
42.Disposition of stright Àõ+Âó+Ñ=0, åñëè À=0, Ñ  0: !!!!! parallel to axis ÎÓ
44.Equalization of parabola, that symmetrical relative to the axis coordinates: !!!!!!! 0: !!!!! parallel to axis ÎÓ
44.Equalization of parabola, that symmetrical relative to the axis coordinates: !!!!!!! 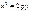 46.Equalization of parabola directrix: !!!!!!!!!
46.Equalization of parabola directrix: !!!!!!!!!  48.Coordinates of focus F parabola: !!!!!!!!
48.Coordinates of focus F parabola: !!!!!!!!  49.Coordinates of focus F parabola
49.Coordinates of focus F parabola 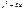 : !!!!!!!!!! : !!!!!!!!!! 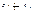 50.Equalization of directrix parabola
50.Equalization of directrix parabola 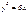 : !!!!!!!!! : !!!!!!!!! 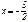 53.Canonical equalization, and distance between the focuses equal 8 ad small axle b=3:
53.Canonical equalization, and distance between the focuses equal 8 ad small axle b=3:
 54.Canonical equalization of ellipse, where large axle à=6 , concentricity.
54.Canonical equalization of ellipse, where large axle à=6 , concentricity.  =0,5: =0,5: 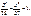 59.Find an element Ñ23 matrix Ñ=ÀÂ, if
59.Find an element Ñ23 matrix Ñ=ÀÂ, if 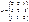 , ,  : !!!!!!! 10
61.Find an element Ñ33 matrix Ñ=ÀÂ, if : !!!!!!! 10
61.Find an element Ñ33 matrix Ñ=ÀÂ, if  , ,  : !!!!!! 2
62.If the determiner square matrix equals zero, she called: !!!!!!!!!!! Singular.
63.If the determiner if square matrix is not equal zero, she called:
Singular.
Nonsingular.
64.The system of linear equalizations is calling compatible, if: !!!!! it has only one solution.
65.n – unknown quantity, m – quantity of the equalization of the system. What kind of condition contribute application the Kramer’s rule? !!!!!!!!!!!!! m = n
66.Coordinates of focus F parabola : !!!!!! 2
62.If the determiner square matrix equals zero, she called: !!!!!!!!!!! Singular.
63.If the determiner if square matrix is not equal zero, she called:
Singular.
Nonsingular.
64.The system of linear equalizations is calling compatible, if: !!!!! it has only one solution.
65.n – unknown quantity, m – quantity of the equalization of the system. What kind of condition contribute application the Kramer’s rule? !!!!!!!!!!!!! m = n
66.Coordinates of focus F parabola  : !!!!!!!!!!!!! : !!!!!!!!!!!!! 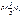 67.If the equalization’ system doesn’t have solution, then the system is calling: Incompatible
68.If in the Kramer’s method D=0, Dõ¹0, then a system: !!!!!!!!! Incompatible .
69.How is located the straight Àõ+Âó+Ñ=0, if Â=0, ѹ0: !!!!!!! Parallel to axis ÎÓ.
70. Formula of the calculus of the distance from point Ì(õ1,ó1) to the straight Àõ+Âó+Ñ=0:
67.If the equalization’ system doesn’t have solution, then the system is calling: Incompatible
68.If in the Kramer’s method D=0, Dõ¹0, then a system: !!!!!!!!! Incompatible .
69.How is located the straight Àõ+Âó+Ñ=0, if Â=0, ѹ0: !!!!!!! Parallel to axis ÎÓ.
70. Formula of the calculus of the distance from point Ì(õ1,ó1) to the straight Àõ+Âó+Ñ=0:
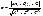 71. In what meanings à and â these straights àõ-2ó-1=0, 6õ-4ó-â=0 are parallel: !!!! à=3, â
71. In what meanings à and â these straights àõ-2ó-1=0, 6õ-4ó-â=0 are parallel: !!!! à=3, â  2.
72.In what meanings à and â these straights ó = àõ+2, ó = 5õ - â are parallel: !!!! à= 5, â 2.
72.In what meanings à and â these straights ó = àõ+2, ó = 5õ - â are parallel: !!!! à= 5, â  -2.
73.How is located the straight Àõ+Âó+Ñ=0, if A=0 !!!!! Parallel to the axis ÎÕ.
74.How is located the straight Àõ+Âó+Ñ=0, if A=C=0: !!!! coincides with the axis ÎÕ.
75.How is located the straight Àõ+Âó+Ñ=0, if B=C=0: !!!! Coincides with the axis ÎÓ.
76.Transpose is the matrix when: !!!!!! permutation rows and columns.
77.Sho the formula derivative function y=arccosx: -2.
73.How is located the straight Àõ+Âó+Ñ=0, if A=0 !!!!! Parallel to the axis ÎÕ.
74.How is located the straight Àõ+Âó+Ñ=0, if A=C=0: !!!! coincides with the axis ÎÕ.
75.How is located the straight Àõ+Âó+Ñ=0, if B=C=0: !!!! Coincides with the axis ÎÓ.
76.Transpose is the matrix when: !!!!!! permutation rows and columns.
77.Sho the formula derivative function y=arccosx:
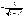 Âîïðîñ ¹ 80
Find the matrix Õ, that satisfy the fellow conditions: 2À+Õ=Â where: À=
Âîïðîñ ¹ 80
Find the matrix Õ, that satisfy the fellow conditions: 2À+Õ=Â where: À=  Â= Â=  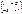 83.Expression of the polar coordinates of the point M in rectangular coordinates:
83.Expression of the polar coordinates of the point M in rectangular coordinates:
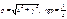 . .
|
84.Expression of the polar coordinates of the point M in rectangular coordinates:
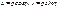 85.The general equation of second degree:
Ax2+Bõy+Có2=+Dx+Ey+F=0.
96.Compute the multiplication of the matrixes ÀÂ, if À=
85.The general equation of second degree:
Ax2+Bõy+Có2=+Dx+Ey+F=0.
96.Compute the multiplication of the matrixes ÀÂ, if À=  Â= Â= 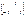 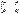 136.If the items are below the main diagonal are zero, then the square matrix is called:
triangular.
139.B as a matrix of four laboratory feeding birds in two different types of food:
136.If the items are below the main diagonal are zero, then the square matrix is called:
triangular.
139.B as a matrix of four laboratory feeding birds in two different types of food:
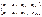 148.Determination of the identity matrix:
diagonal elements are composed of units of the remaining zeros.
149. What condition is required to add two matrices:
the same dimension matrices.
150.What condition must be fulfilled for the multiplication of two matrices:
number of columns of the first matrix equals the number of rows of the second matrix.
151.In which case the system of equations is called homogeneous:
all the free terms are equal to zero.
163.Calculate determine the 3rd order:
148.Determination of the identity matrix:
diagonal elements are composed of units of the remaining zeros.
149. What condition is required to add two matrices:
the same dimension matrices.
150.What condition must be fulfilled for the multiplication of two matrices:
number of columns of the first matrix equals the number of rows of the second matrix.
151.In which case the system of equations is called homogeneous:
all the free terms are equal to zero.
163.Calculate determine the 3rd order: 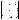 16.
174.Calculate the determinant 16.
174.Calculate the determinant 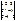 : 2.
176.In which case the determinant does not change
if interchange rows and columns with the same number
177.An additional determinant of : 2.
176.In which case the determinant does not change
if interchange rows and columns with the same number
177.An additional determinant of 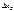 : :  is obtained by substituting the second column of free terms.
179.If the determinant of the system is different from zero, then the solution of the system:
is obtained by substituting the second column of free terms.
179.If the determinant of the system is different from zero, then the solution of the system:  182.Solution of the system
182.Solution of the system 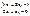 are:
x1=1, x2=-2.
x1=-1, x2=2.
190.A square matrix A n-th order is called degenerate if: detA=0 are:
x1=1, x2=-2.
x1=-1, x2=2.
190.A square matrix A n-th order is called degenerate if: detA=0
|
1.Solve the system if equations: 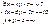 !!!!!! (-4; 2; -1).
2.The point of intersection of the circumference (õ-4)2+ó2=25: !!!!!! Ì(0; !!!!!! (-4; 2; -1).
2.The point of intersection of the circumference (õ-4)2+ó2=25: !!!!!! Ì(0;  3)
3.Show the equation of circumference, where the center is situated in point (2;-3) and circumference passes through the point (5;1): !!!!!!!!!!! (õ-2)2+(ó+3)2=25.
4.The distance between centers of the circumferences õ2+ó2=16 and (õ+3)2+(ó+4)2=25: !!!!! 5
18.Abscissa of the circumference’s point õ2+(ó+4)2=41 and the point on it with ordinate equals zero: !!!!!! 5
19.The curve, specified by equalization (õ-à)2+(ó-b)2=r2: !!!!!!! Circumference.
20.Ordinate of the circumference’s point (õ+3)2+ó2=25, where abscissa equals zero: !!!!! 4
21. A canonical equalization of the ellipse: !!!! 3)
3.Show the equation of circumference, where the center is situated in point (2;-3) and circumference passes through the point (5;1): !!!!!!!!!!! (õ-2)2+(ó+3)2=25.
4.The distance between centers of the circumferences õ2+ó2=16 and (õ+3)2+(ó+4)2=25: !!!!! 5
18.Abscissa of the circumference’s point õ2+(ó+4)2=41 and the point on it with ordinate equals zero: !!!!!! 5
19.The curve, specified by equalization (õ-à)2+(ó-b)2=r2: !!!!!!! Circumference.
20.Ordinate of the circumference’s point (õ+3)2+ó2=25, where abscissa equals zero: !!!!! 4
21. A canonical equalization of the ellipse: !!!! 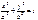 22.The curve, set by the equalization
22.The curve, set by the equalization 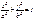 : !!!!!!!!!!! Ellipse.
23.The point of intersection the hyperbola õ2-4ó2=16 with the axis of abscissas: !!! Ì( ±4; 0).
27.Equalizations of asymptotes of the hyperbola : !!!!!!!!!!! Ellipse.
23.The point of intersection the hyperbola õ2-4ó2=16 with the axis of abscissas: !!! Ì( ±4; 0).
27.Equalizations of asymptotes of the hyperbola 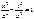 : !!!!! : !!!!! 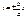 28.Equalizations of asymptotes of the hyperbola
28.Equalizations of asymptotes of the hyperbola  : !!!! : !!!! 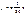 .
29.Describe the distance d from origin coordinates to point Ì(õ;ó): !!!!! .
29.Describe the distance d from origin coordinates to point Ì(õ;ó): !!!!! 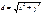 ;
33.Length of the cutoff ÀÂ with the coordinates À(õ1;ó1) and Â(õ2;ó2): ;
33.Length of the cutoff ÀÂ with the coordinates À(õ1;ó1) and Â(õ2;ó2):  36.Coordinates of the interval’s midpoint ÀÂ, À(õ1;ó1)and Â(õ2;ó2):
36.Coordinates of the interval’s midpoint ÀÂ, À(õ1;ó1)and Â(õ2;ó2):  .
39.A rectangle prescribed by coordinates of its apices À(1; 1), Â(8;-5), Ñ(3;5).Point Ì the midpoint of the leg ÀÑ. Length of the median ÂÌ equals: !!!!!! 10
40.Disposition of straight Àõ+Âó+Ñ=0, if Â=0, Ñ .
39.A rectangle prescribed by coordinates of its apices À(1; 1), Â(8;-5), Ñ(3;5).Point Ì the midpoint of the leg ÀÑ. Length of the median ÂÌ equals: !!!!!! 10
40.Disposition of straight Àõ+Âó+Ñ=0, if Â=0, Ñ 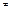 0: !!!!!! parallel to axis ÎÕ
41. Angular coefficient of the straight 2,5ó-5õ+5=0: !!!! 2
42.Disposition of stright Àõ+Âó+Ñ=0, åñëè À=0, Ñ 0: !!!!!! parallel to axis ÎÕ
41. Angular coefficient of the straight 2,5ó-5õ+5=0: !!!! 2
42.Disposition of stright Àõ+Âó+Ñ=0, åñëè À=0, Ñ  0: !!!!! parallel to axis ÎÓ
44.Equalization of parabola, that symmetrical relative to the axis coordinates: !!!!!!! 0: !!!!! parallel to axis ÎÓ
44.Equalization of parabola, that symmetrical relative to the axis coordinates: !!!!!!! 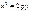 46.Equalization of parabola directrix: !!!!!!!!!
46.Equalization of parabola directrix: !!!!!!!!!  48.Coordinates of focus F parabola: !!!!!!!!
48.Coordinates of focus F parabola: !!!!!!!!  49.Coordinates of focus F parabola
49.Coordinates of focus F parabola 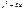 : !!!!!!!!!! : !!!!!!!!!! 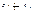 50.Equalization of directrix parabola
50.Equalization of directrix parabola 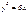 : !!!!!!!!! : !!!!!!!!! 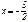 53.Canonical equalization, and distance between the focuses equal 8 ad small axle b=3:
53.Canonical equalization, and distance between the focuses equal 8 ad small axle b=3:
 54.Canonical equalization of ellipse, where large axle à=6 , concentricity.
54.Canonical equalization of ellipse, where large axle à=6 , concentricity.  =0,5: =0,5: 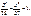 59.Find an element Ñ23 matrix Ñ=ÀÂ, if
59.Find an element Ñ23 matrix Ñ=ÀÂ, if 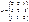 , ,  : !!!!!!! 10
61.Find an element Ñ33 matrix Ñ=ÀÂ, if : !!!!!!! 10
61.Find an element Ñ33 matrix Ñ=ÀÂ, if  , ,  : !!!!!! 2
62.If the determiner square matrix equals zero, she called: !!!!!!!!!!! Singular.
63.If the determiner if square matrix is not equal zero, she called:
Singular.
Nonsingular.
64.The system of linear equalizations is calling compatible, if: !!!!! it has only one solution.
65.n – unknown quantity, m – quantity of the equalization of the system. What kind of condition contribute application the Kramer’s rule? !!!!!!!!!!!!! m = n
66.Coordinates of focus F parabola : !!!!!! 2
62.If the determiner square matrix equals zero, she called: !!!!!!!!!!! Singular.
63.If the determiner if square matrix is not equal zero, she called:
Singular.
Nonsingular.
64.The system of linear equalizations is calling compatible, if: !!!!! it has only one solution.
65.n – unknown quantity, m – quantity of the equalization of the system. What kind of condition contribute application the Kramer’s rule? !!!!!!!!!!!!! m = n
66.Coordinates of focus F parabola  : !!!!!!!!!!!!! : !!!!!!!!!!!!! 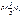 67.If the equalization’ system doesn’t have solution, then the system is calling: Incompatible
68.If in the Kramer’s method D=0, Dõ¹0, then a system: !!!!!!!!! Incompatible .
69.How is located the straight Àõ+Âó+Ñ=0, if Â=0, ѹ0: !!!!!!! Parallel to axis ÎÓ.
70. Formula of the calculus of the distance from point Ì(õ1,ó1) to the straight Àõ+Âó+Ñ=0:
67.If the equalization’ system doesn’t have solution, then the system is calling: Incompatible
68.If in the Kramer’s method D=0, Dõ¹0, then a system: !!!!!!!!! Incompatible .
69.How is located the straight Àõ+Âó+Ñ=0, if Â=0, ѹ0: !!!!!!! Parallel to axis ÎÓ.
70. Formula of the calculus of the distance from point Ì(õ1,ó1) to the straight Àõ+Âó+Ñ=0:
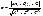 71. In what meanings à and â these straights àõ-2ó-1=0, 6õ-4ó-â=0 are parallel: !!!! à=3, â
71. In what meanings à and â these straights àõ-2ó-1=0, 6õ-4ó-â=0 are parallel: !!!! à=3, â  2.
72.In what meanings à and â these straights ó = àõ+2, ó = 5õ - â are parallel: !!!! à= 5, â 2.
72.In what meanings à and â these straights ó = àõ+2, ó = 5õ - â are parallel: !!!! à= 5, â  -2.
73.How is located the straight Àõ+Âó+Ñ=0, if A=0 !!!!! Parallel to the axis ÎÕ.
74.How is located the straight Àõ+Âó+Ñ=0, if A=C=0: !!!! coincides with the axis ÎÕ.
75.How is located the straight Àõ+Âó+Ñ=0, if B=C=0: !!!! Coincides with the axis ÎÓ.
76.Transpose is the matrix when: !!!!!! permutation rows and columns.
77.Sho the formula derivative function y=arccosx: -2.
73.How is located the straight Àõ+Âó+Ñ=0, if A=0 !!!!! Parallel to the axis ÎÕ.
74.How is located the straight Àõ+Âó+Ñ=0, if A=C=0: !!!! coincides with the axis ÎÕ.
75.How is located the straight Àõ+Âó+Ñ=0, if B=C=0: !!!! Coincides with the axis ÎÓ.
76.Transpose is the matrix when: !!!!!! permutation rows and columns.
77.Sho the formula derivative function y=arccosx:
 Âîïðîñ ¹ 80
Find the matrix Õ, that satisfy the fellow conditions: 2À+Õ=Â where: À=
Âîïðîñ ¹ 80
Find the matrix Õ, that satisfy the fellow conditions: 2À+Õ=Â where: À=  Â= Â=  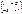 83.Expression of the polar coordinates of the point M in rectangular coordinates:
83.Expression of the polar coordinates of the point M in rectangular coordinates:
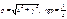 . .
|
84.Expression of the polar coordinates of the point M in rectangular coordinates:
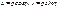 85.The general equation of second degree:
Ax2+Bõy+Có2=+Dx+Ey+F=0.
96.Compute the multiplication of the matrixes ÀÂ, if À=
85.The general equation of second degree:
Ax2+Bõy+Có2=+Dx+Ey+F=0.
96.Compute the multiplication of the matrixes ÀÂ, if À=  Â= Â= 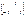 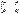 136.If the items are below the main diagonal are zero, then the square matrix is called:
triangular.
139.B as a matrix of four laboratory feeding birds in two different types of food:
136.If the items are below the main diagonal are zero, then the square matrix is called:
triangular.
139.B as a matrix of four laboratory feeding birds in two different types of food:
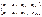 148.Determination of the identity matrix:
diagonal elements are composed of units of the remaining zeros.
149. What condition is required to add two matrices:
the same dimension matrices.
150.What condition must be fulfilled for the multiplication of two matrices:
number of columns of the first matrix equals the number of rows of the second matrix.
151.In which case the system of equations is called homogeneous:
all the free terms are equal to zero.
163.Calculate determine the 3rd order:
148.Determination of the identity matrix:
diagonal elements are composed of units of the remaining zeros.
149. What condition is required to add two matrices:
the same dimension matrices.
150.What condition must be fulfilled for the multiplication of two matrices:
number of columns of the first matrix equals the number of rows of the second matrix.
151.In which case the system of equations is called homogeneous:
all the free terms are equal to zero.
163.Calculate determine the 3rd order: 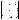 16.
174.Calculate the determinant 16.
174.Calculate the determinant 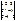 : 2.
176.In which case the determinant does not change
if interchange rows and columns with the same number
177.An additional determinant of : 2.
176.In which case the determinant does not change
if interchange rows and columns with the same number
177.An additional determinant of 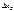 : :  is obtained by substituting the second column of free terms.
179.If the determinant of the system is different from zero, then the solution of the system:
is obtained by substituting the second column of free terms.
179.If the determinant of the system is different from zero, then the solution of the system:  182.Solution of the system
182.Solution of the system 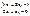 are:
x1=1, x2=-2.
x1=-1, x2=2.
190.A square matrix A n-th order is called degenerate if: detA=0 are:
x1=1, x2=-2.
x1=-1, x2=2.
190.A square matrix A n-th order is called degenerate if: detA=0
|
Date: 2015-12-24; view: 1270
| <== previous page | | | next page ==> |
| | | Vocabulary Follow-Up |