Power use and propulsive efficiency

Delta-v and propellant

Exhausting the entire usable propellant of a spacecraft through the engines in a straight line in free space would produce a net velocity change to the vehicle; this number is termed 'delta-v' (Δv).

If the exhaust velocity is constant then the total Δv of a vehicle can be calculated using the rocket equation, where M is the mass of propellant, P is the mass of the payload (including the rocket structure), and v_e is the velocity of the rocket exhaust. This is known as the Tsiolkovsky rocket equation:

For historical reasons, as discussed above, v_e is sometimes written as

v_e = I_spg_o

where I_sp is the specific impulse of the rocket, measured in seconds, and g_o is the gravitational acceleration at sea level.

For a high delta-v mission, the majority of the spacecraft's mass needs to be reaction mass. Since a rocket must carry all of its reaction mass, most of the initially-expended reaction mass goes towards accelerating reaction mass rather than payload. If the rocket has a payload of mass P, the spacecraft needs to change its velocity by Δv, and the rocket engine has exhaust velocity v_e, then the mass M of reaction mass which is needed can be calculated using the rocket equation and the formula for I_sp:

For Δv much smaller than v_e, this equation is roughly linear, and little reaction mass is needed. If Δv is comparable to v_e, then there needs to be about twice as much fuel as combined payload and structure (which includes engines, fuel tanks, and so on). Beyond this, the growth is exponential; speeds much higher than the exhaust velocity require very high ratios of fuel mass to payload and structural mass.

For a mission, for example, when launching from or landing on a planet, the effects of gravitational attraction and any atmospheric drag must be overcome by using fuel. It is typical to combine the effects of these and other effects into an effective mission delta-v. For example a launch mission to low Earth orbit requires about 9.3–10 km/s delta-v. These mission delta-vs are typically numerically integrated on a computer.

Some effects such as Oberth effect can only be significantly utilised by high thrust engines such as rockets, i.e. engines that can produce a high g-force (thrust per unit mass, equal to delta-v per unit time).

Power use and propulsive efficiency

For all reaction engines (such as rockets and ion drives) some energy must go into accelerating the reaction mass. Every engine will waste some energy, but even assuming 100% efficiency, to accelerate an exhaust the engine will need energy amounting to

his energy is not necessarily lost- some of it usually ends up as kinetic energy of the vehicle, and the rest is wasted in residual motion of the exhaust.

Due to energy carried away in the exhaust the energy efficiency of a reaction engine varies with the speed of the exhaust relative to the speed of the vehicle, this is called propulsive efficiency

Comparing the rocket equation (which shows how much energy ends up in the final vehicle) and the above equation (which shows the total energy required) shows that even with 100% engine efficiency, certainly not all energy supplied ends up in the vehicle - some of it, indeed usually most of it, ends up as kinetic energy of the exhaust.

The exact amount depends on the design of the vehicle, and the mission. However there are some useful fixed points:

-if the I_sp is fixed, for a mission delta-v, there is a particular I_sp that minimises the overall energy used by the rocket. This comes to an exhaust velocity of about ⅔ of the mission delta-v (see the energy computed from the rocket equation). Drives with a specific impulse that is both high and fixed such as Ion thrusters have exhaust velocities that can be enormously higher than this ideal for many missions.

-if the exhaust velocity can be made to vary so that at each instant it is equal and opposite to the vehicle velocity then the absolute minimum energy usage is achieved. When this is achieved, the exhaust stops in space and has no kinetic energy; and the propulsive efficiency is 100%- all the energy ends up in the vehicle (in principle such a drive would be 100% efficient, in practice there would be thermal losses from within the drive system and residual heat in the exhaust). However in most cases this uses an impractical quantity of propellant, but is a useful theoretical consideration. Anyway the vehicle has to move before the method can be applied.

Some drives (such as VASIMR or Electrodeless plasma thruster) actually can significantly vary their exhaust velocity. This can help reduce propellant usage or improve acceleration at different stages of the flight. However the best energetic performance and acceleration is still obtained when the exhaust velocity is close to the vehicle speed. Proposed ion and plasma drives usually have exhaust velocities enormously higher than that ideal (in the case of VASIMR the lowest quoted speed is around 15000 m/s compared to a mission delta-v from high Earth orbit to Mars of about 4000m/s).

It might be thought that adding power generation capacity is helpful, and while initially this can improve performance, this inevitably increases the weight of the power source, and eventually the mass of the power source and the associated engines and propellant dominates the weight of the vehicle, and then adding more power gives no significant improvement.

For, although solar power and nuclear power are virtually unlimited sources of energy, the maximum power they can supply is substantially proportional to the mass of the powerplant (i.e. specific powertakes a largely constant value which is dependent on the particular powerplant technology). For any given specific power, with a large v_e which is desirable to save propellant mass, it turns out that the maximum acceleration is inversely proportional to v_e. Hence the time to reach a required delta-v is proportional to v_e. Thus the latter should not be too large.

Energy

In the ideal case m₁ is useful payload and m₀ − m₁ is reaction mass (this corresponds to empty tanks having no mass, etc.). The energy required can simply be computed as

This corresponds to the kinetic energy the expelled reaction mass would have at a speed equal to the exhaust speed. If the reaction mass had to be accelerated from zero speed to the exhaust speed, all energy produced would go into the reaction mass and nothing would be left for kinetic energy gain by the rocket and payload. However, if the rocket already moves and accelerates (the reaction mass is expelled in the direction opposite to the direction in which the rocket moves) less kinetic energy is added to the reaction mass. To see this, if, for example, v_e=10 km/s and the speed of the rocket is 3 km/s, then the speed of a small amount of expended reaction mass changes from 3 km/s forwards to 7 km/s rearwards. Thus, while the energy required is 50 MJ per kg reaction mass, only 20 MJ is used for the increase in speed of the reaction mass. The remaining 30 MJ is the increase of the kinetic energy of the rocket and payload.

In general:

Thus the specific energy gain of the rocket in any small time interval is the energy gain of the rocket including the remaining fuel, divided by its mass, where the energy gain is equal to the energy produced by the fuel minus the energy gain of the reaction mass. The larger the speed of the rocket, the smaller the energy gain of the reaction mass; if the rocket speed is more than half of the exhaust speed the reaction mass even loses energy on being expelled, to the benefit of the energy gain of the rocket; the larger the speed of the rocket, the larger the energy loss of the reaction mass.

We have

where is the specific energy of the rocket (potential plus kinetic energy) and Δv is a separate variable, not just the change in v. In the case of using the rocket for deceleration, i.e. expelling reaction mass in the direction of the velocity, v should be taken negative.

The formula is for the ideal case again, with no energy lost on heat, etc. The latter causes a reduction of thrust, so it is a disadvantage even when the objective is to lose energy (deceleration).

If the energy is produced by the mass itself, as in a chemical rocket, the fuel value has to be 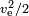, where for the fuel value also the mass of the oxidizer has to be taken into account. A typical value isv_e = 4.5 km/s, corresponding to a fuel value of 10.1 MJ/kg. The actual fuel value is higher, but much of the energy is lost as waste heat in the exhaust that the nozzle was unable to extract.

The required energy E is

Conclusions:

-for a given Δv, the minimum energy is needed if v_e = 0.6275Δv, requiring an energy of

E = 0.772m₁(Δv)².

Starting from zero speed this is 54.4 % more than just the kinetic energy of the payload. In this optimal case the initial mass is 4.92 times the final mass.

These results apply for a fixed exhaust speed.

Due to the Oberth effect, and starting from a nonzero speed the required potential energy needed from the propellant may be less than the increase in energy in the vehicle and payload. This can be the case when the reaction mass has a lower speed after being expelled than before- rockets are able to liberate some or all of the initial kinetic energy of the propellant.

Also, for a given objective such as moving from one orbit to another, the required Δv may depend greatly on the rate at which the engine can produce Δv and maneuvers may even be impossible if that rate is too low. For example, a launch to LEO normally requires a Δv of ca. 9.5 km/s (mostly for the speed to be acquired), but if the engine could produce Δv at a rate of only slightly more than g, it would be a slow launch requiring altogether a very large Δv (think of hovering without making any progress in speed or altitude, it would cost a Δv of 9.8 m/s each second). If the possible rate is only gor less, the maneuver cannot be carried out at all with this engine.

The power is given by

where F is the thrust and a the acceleration due to it. Thus the theoretically possible thrust per unit power is 2 divided by the specific impulse in m/s. The thrust efficiency is the actual thrust as percentage of this.

If e.g. solar power is used this restricts a; in the case of a large v_e the possible acceleration is inversely proportional to it, hence the time to reach a required delta-v is proportional to v_e; with 100% efficiency

Examples:

-power 1000 W, mass 100 kg, Δv= 5 km/s, v_e= 16 km/s, takes 1.5 months.

-power 1000 W, mass 100 kg, Δv= 5 km/s, v_e= 50 km/s, takes 5 months.

Thus v_e should not be too large.

Date: 2015-12-18; view: 1062