Surfaces of the second order in the space

L E C T U R E 5

Sphere.In Cartesian system of coordinates a sphere having the center in point and radius is determined by the equation (canonic form): .

Example. Find the coordinates of center and radius of a sphere given by the following equation:

Solution: Find canonic form of this sphere: , or

Consequently, the center of the sphere is and .

Cylindrical and conic surfaces.Let a system of coordinates be given. We say that a curve in the space be given parametrically by vector-function (or in coordinate form where 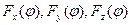are continuous functions of defined for if 1) for every the point lies on ; 2) for every point lying on there is such that holds. Sometimes a curve in the space is given by an equation that is obtained by excluding parameter from the coordinate form.

Example. In Cartesian system of coordinates a curve of the second order is a line.

Let some curve which we will name directing be given.

Let's draw through each point of the directing curve a straight line named generatrix that is parallel to some non-zero vector . The set of all points of the space lying on generatrices of a given type is called a cylindrical surface.

cylindrical case conic case

Compose an equation of cylindrical surface in common form. In the introduced notations , but by definition of cylindrical surface and consequently, an equation of cylindrical surface in vector form: . In coordinate form after excluding we obtain .

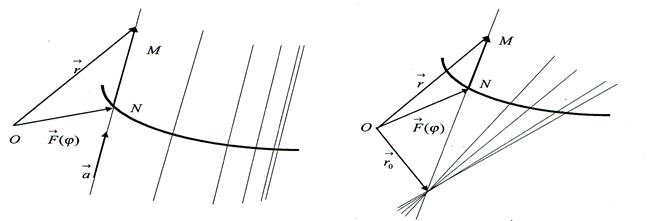
Let’s draw through each point of the directing curve a straight line (named generatrix) passing through some fixed non-belonging to the curve point (named the vertex). The set of all points of the space lying on generatrices of a given type is called a conic surface.

Compose an equation of conic surface in common form. In the introduced notations , but by definition of conic surface and consequently, an equation of conic surface in vector form: . In coordinate form after excluding we obtain .

An equation of the form determines in the space a cylindrical surface at which generatrices are parallel to 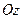. Analogously, an equation 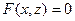determines a cylindrical surface with generatrices that are parallel to , and – a cylindrical surface with generatrices that are parallel to .

Canonic equations of cylinders of the second order are the following:

Elliptic cylinder – , hyperbolic cylinder – , parabolic cylinder – .

Generatrices of all these cylinders defined by these equations are parallel to 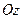, and the directing curve is the corresponding curve of the second order (ellipse, hyperbola, parabola) lying in . At a cone and an elliptic cylinder are called a circular cone and a circular cylinder.

One should remember that a curve in the space can be given as a line of intersecting two surfaces. For example, equations of the directing curve of an elliptic cylinder, i.e. an equation of ellipse in plane has the form

An equation of cone of the second order with vertex in the origin of coordinates of which the axis is 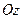is written in the form . Analogously, the equations and are equations of cones of the second order with vertex in the origin of coordinates of which the axes are and .

Example. Which surface do the following equations determine in the space: a) ; b) ?

Solution: a) The equation determines a parabolic cylinder with generatrices that are parallel to 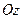. The directing curve of the cylindrical surface is the parabola .

b) The equation can be represented as 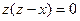and is decomposed into two equations: and , i.e. it determines two planes: and the plane passing through .

Date: 2015-12-18; view: 969