
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
FOR THE FULFILL THE OVERALL OBJECTIVE STUDENT SHOULD BE ABLE
Types of algorithms. Examples. Algorithm diagram.
The algorithm is a system of the formal rules which accurately and single-digit contour sequence of actions of enumerative process from initial data to required result. There are three basic structures of algorithm:
- The linear algorithms
The algorithm in which all stages of the solution of the task are executed strictly sequentially is called the linear. I.e. the linear algorithm is executed in a natural order of its writing and doesn't contain ramifyings and repetitions.
- Algorithms of branching structure
Algorithm of branching structure we will call such algorithm which one of several possible ways (options) of calculating process is selected. Sign of branching algorithm is existence of operations of the conditional branch when there is a check of truth of some logical expression (a checked condition) and depending on truth or falsehood of a checked condition for execution this or that branch of algorithm is selected
- Cyclic algorithm.
Implements repetition of some actions. Differently Cyclic algorithms include cycles. The sequence of the actions executed repeatedly, each time is called as a cycle in case of new parameter values.
The algorithm diagram the flowchart) - the graphics image of its structure in which each process step of data handling is presented in the form of different geometrical figures (units).
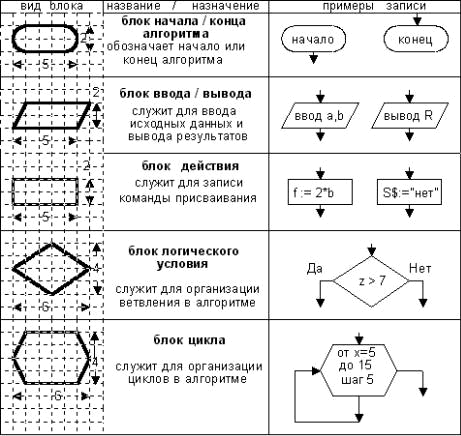
unit of the beginning/the end, unit of input-output, unit of action, unit of logical action, unit of a cycle
Symmetry. 5. _________ In the early days of X-ray analysis, when the ionic compounds that were being studied often had a high symmetry this fact was of great assistance in arriving at a solution. The possible schemes of symmetry are limited by geometry, just as the possible number of regular solid figures are limited, although in the case of crystals symmetries the number, 230, is quite large. Symmetry axes and symmetry planes can be identified by nothing regular absences of diffracted - wave orders; the presence or absence of symmetry centers can be determined by a statistical survey of intensities, as was first shown by A.T. Wilson; crystals with symmetry centers characteristically have many more weak reflections than crystals with no symmetry centers.
6. _________ Optically active molecules can have two forms, one of which is the reflection of the other (dextro and levo forms of the chemists). In general when the waves scattered by the atoms have phases as if coming from atomic centers, these two forms give identical X-ray diffraction, that is, the reflection from the right-hand side has the same amplitude as that from the left, although the phase is reversed. 7. _________The atom scatters as if at one location for the one side and at another location for the two other side so that two resultant amplitudes are different. This enables dextro and levo to be distinguished, for instance, in the classic case of a tetrahedron with four different corners, one could tell for each orientation whether one was looking at an appex or a base. I.M. Biyvoet was the first to distinguish between dextro and levo forms of the ion. There was a 50:50 chance, that the traditional chemical convention for representing dextro and levo was correct; luckily it turned out to be right.
| Task 4. | Match the words in column A with their Ukrainian equivalents from column B: | ||||
| A | B | ||||
| symmetry centers | a) | ||||
| dextro forms | b) | ||||
| tetrahedron | c) | ||||
| to commingle | d) | ||||
| orientation | e) | ||||
| resultant amplitude | f) | ||||
| glancing angle | g) | ||||
| crystal chemistry | h) | ||||
| path difference | i) | ||||
| to determine | j) | ||||
| reflected wave | k) | ||||
| anisotropy | l) | ||||
| absorption edge | m) | ||||
| wavetrains | n) | ||||
| Task 5. | Give the Ukrainian equivalents to the following words and word combinations: |
monochromatic (uniform wavelength), successive sheets, wavetrains, a strong reflected beam, glancing angle, initial adventure, interpretational techniques, crystalline penicillin, mathematical analysis of anisotropy, preferred orientations, alias textures, inextricably commingled, a three-dimensional scaffolding, uniquely determined, symmetry planes, absorbtion edge.
| Task 6. | Answer the following questions: |
| 1. What is the easiest way to approach the optical problem of X-ray diffraction? | |
| 2. When will the wavelength combine to form a reflected beam and what is its geometric interpretation? | |
| 3. What is the pattern of every crystal? | |
| 4. How can symmetry axes and symmetry planes be identified? | |
| 5. How can the presence or absence of symmetry centers be determined? | |
| 6. What forms can active molecules have optically? |
| Task 7. | Pick up the key words from the text “Auger Electron Spectroscopy” and make up your own sentences with them. |
| Task 8. | Write down 5-7 sentences to prove or disapprove the statement: Crystallography is a very broad science. |
| Unit 8 | The Fourier Method |
| Task 1. | Before reading think about the answers to these questions. Then read the text “The Fourier Method” and check whether your guesses are correct: |
1. Can you give the definition of the Fourier Method?
2. What science is Fourier Method applied in?
| Task 2. | Scan the text “The Fourier Method”. Seven sentences have been removed from the text. Choose from the sentences (A-H) the one which fits each gap (1-7). There is one extra sentence which you do not need to use. There is an example at the beginning (1). |
| A | The second approach was outlined by Balzar and Enzo among other authors and is based on the convolution profile-fitting method as a tool for the extraction of the intrinsic physical diffraction line profile. |
| B | Optically active molecules can have two forms, one of which is the reflection of the other. |
| C | They are often called size-strain analyses and usually include the evaluation of average crystallite sizes, crystallite size distributions, microstrains, dislocation densities and stacking fault probabilities. |
| D | So far the crystal has been regarded as a pattern of atoms each of which scatters X-rays as if from its centre with an efficiency determined by Hartree’s F curves. |
| E | Each element of the series is a set of electron sheets, or strata, that vary periodically in density, and if the amplitudes and phases of these sheets (which criss-cross in all directions) are known, they can be added and the result is a plot of the density distribution. |
| F | This method states that the Fourier coefficients for intrinsic physical line profile are the product of two terms: the size and the strain coefficient. |
| G | The investigator seeks to map this continuous distribution and if he is successful, he can then recognize the positions of the atoms by noting where the electron density rises to pick values. |
| H | The size and strain coefficients are afterwards numerically determined following Warren-Averbach method. |
| Task 3. | Read the text “The Fourier Method” and find English equivalents to the following words and word combinations: |
THE FOURIER METHOD
In the last five decades, defect structure analysis of polycrystalline materials by X-ray powder diffraction technique has been able to cover a number of lattice imperfections. 1. ____C____ They are generally based on two different approaches and have been incorporating an impressively high number of modifications and nuances that is too hard to mention all of them. Both approaches require a twofold task: the determination of the intrinsic (pure) physical diffraction line profile of the sample and, then, the extraction of the lattice imperfection parameters.
The first highly elaborated approach of size/strain analysis is Warren-Averbach method (known also as a Warren-Averbach-Bertaut method) which employs the deconvolution Fourier-transform method (known also as the Stokes method) for the determination of the intrinsic physical line profile, followed by the Fourier method for evaluation of lattice imperfections. 2. _________ The coefficients are numerically calculated. The method was initially proposed for application in the field of metals and alloys, but rapidly was extend to the area of ceramic and also polymer materials.
3. _________ The intrinsic line parameters extract in this manner, such as 200 diffraction line positions, full width at a half maximum (FWHM), integral breadths and others, that define diffraction line shapes, are further used to calculate the Fourier transforms of intrinsic diffraction lines.
Balzar’s method uses the Voigt function and its Fourier transform to describe the intrinsic line profile, which is used to calculate both the size and strain coefficients proposed by Warren and Averbach. The advantages of Balzar’s method are that the Voigt function Fourier transform has an analytical form and the convolution of two Voigt functions is also a Voigt function, so size and strain coefficients could be analytically determined.
Enzo’s method uses a pseudo-Voigt function and its Fourier transform for the description of the intrinsic line profile. 4. _________
The acceptance of the convolution profile-fitting methods in the materials science community is very high due to the much less consuming time than the Warren-Averbach method, giving, nonetheless, trustful results. There are numbers of publications on lattice imperfection analyses using the second approach. However, the Warren-Averbach method is still considered as the less biased one, because it does not assume any shape for the diffraction lines. At the other side, the second approach uses some analytical functions to describe the diffraction line shapes. Experimentally it has been showed that in the most cases satisfactory representation of diffraction lines is done by Voigt function, or by some of it approximations, pseudo-Voigt and Pearson VII.
Another method of X-ray analysis attacks the solution of the crystal structure from a quite different angle. 5. _________ The resultant of the waves scattered by these atoms is then compared with the observed amplitude of reflection, the position of the atoms being adjusted to give the best fit. This method was successful as long as the number of atoms in the unit cell was small. As increasingly complex crystals were studied however, it became more and more difficult to try adjustments of so many parameters simultaneously, even when the structure was approximately known. The refining of the structure to get the best fit became extremely laborious.
The Fourier method is in a sense a complete reversal of this process. A structure is treated not as a cluster of atoms put as continuous electron distribution capable of scattering X-rays. 6._________ There is no juggling with the positions of the atoms one by one; the density map shows the best position for all of them, however large their number.
The density distributions are mapped by adding together the terms of a "Fourier series", a mathematical expression that can be used to represent any quantity that varies periodically. Since the crystal is a periodic pattern in three dimensions, the electron density can be represented by a three-dimensional Fourier series. 7. _________
| Task 4. | Match the words in column A with their Ukrainian equivalents from column B: | ||||
| A | B | ||||
| strata | a) | ||||
| cluster of atoms | b) | ||||
| laborious | c) | ||||
| diffraction lines | d) | ||||
| microstrain | e) | ||||
| imperfection | f) | ||||
| powder diffraction | g) | ||||
| criss-cross | h) | ||||
| complete reversal | i) | ||||
| convolution | j) | ||||
| intrinsic diffraction line | k) | ||||
| lattice | l) | ||||
| integral breadth | m) | ||||
| twofold task | n) | ||||
| Task 5. | Give the Ukrainian equivalents to the following words and word combinations: |
powder diffraction technique, size-strain analyses, lattice imperfection parameters, polymer materials, the convolution profile-fitting method, integral breadths, intrinsic diffraction lines, size and strain coefficients, the less biased method, a pattern of atoms, amplitude of reflection, refining of the structure, to become extremely laborious, cluster of atoms, pick values, a set of electron sheets, a plot of the density distribution, stacking fault probabilities.
| Task 6. | Answer the following questions: |
| 1. What do size-strain analyses usually include? |
| 2. What do two approaches of size-strain analyses require? |
| 3. What is the basis for the second approach which was outlined by Balzar and Enzo? |
| 4. What can we use for description of intrinsic line profile? |
| 5. Where is pseudo-Voigt function used? |
| 6. Which approach is more often used and why? |
| 7. What is the method of X-ray analysis? |
| 8. What is Fourier Series? |
| Task 7. | Pick up all the methods mentioned in the text “The Fourier Method” and give a short characteristic to each of them. |
| Task 8. | Write down a plan to the text “The Fourier Method” in the form of questions. |
| Unit 9 | Statistical mechanics |
| Task 1. | Before reading think about the answers to these questions. Then read the text “Statistical mechanics” and check whether your guesses are correct: |
1. Who created the science called statistical mechanics?
2. What scientists contributed greatly to the development of the statistical mechanics?
| Task 2. | Scan the text “Statistical mechanics”. Five sentences have been removed from the text. Choose from the sentences (A-F) the one which fits each gap (1-5). There is one extra sentence which you do not need to use. There is an example at the beginning (1). |
| A | This important field of theory, which has no proper name even today, has become a major domain of research in its own right and has been recognised with a Nobel Prize awarded to Kenneth Wilson in 1982. |
| B | An entire chapter is devoted to the Gibbs/ Boltzmann connection, culminating in a section entitled "Why is statistical mechanics usually attributed to Gibbs and not to Boltzmann?". |
| C | It is Boltzmann’s work which has really made possible the modern flowering of statistical thermodynamics of solids. |
| D | There are numbers of publications on lattice imperfection analyses using the second approach. |
| E | His own contributions to the field were negligible." Naming of phenomena sometimes rewards the wrong person! |
| F | He was the first to recognise that the molecules would not all have the same kinetic energy. |
| Task 3. | Read the text “Statistical mechanics” and find English equivalents to the following words and word combinations: |
STATISTICAL MECHANICS
It is one of the wonders of the history of physics that a rigorous theory of the behaviour of a chaotic assembly of molecules - a gas - preceded by several decades the experimental uncovering of the structure of regular, crystalline solids. Attempts to create a kinetic theory of gases go all the way back to the Swiss mathematician, Daniel Bernouilli, in 1738, followed by John Herapath in 1820 and John James Waterston in 1845. But it fell to the great James Clerk Maxwell in the 1860s to take the first accurate steps - and they were giant steps - in interpreting the pressure-volume-temperature relationship of a gas in terms of a probabilistic (or statistical) analysis of the behaviour of very large populations of mutually colliding molecules -the kinetic theory of gases. 1. ____F____ The Maxwell distribution of kinetic energies of such a population has made his name immortal... even if it had not been immortalised by his electromagnetic equations. The science he created is sometimes called statistical mechanics, sometimes statistical thermodynamics.
For many years this kind of theory was applied to fluids of various kinds, and it became interestingly applicable to solids much later, in 1925, when W. Lenz in Germany, together with his student Ising, created the theory of critical phenomena, which covers phenomena in solids such as ferromagnetism and order-disorder transitions. 2. _________ The issue was whether an array of spins attached to atoms in a regular array would automatically generate spin alignment and ferromagnetism. Ising only managed a theory in one dimension and wrongly surmised that in higher dimensions there would be no ferromagnetism. The many attempts to generalise the theory to two or three dimensions began with Rudolf Peierls in 1936; he showed that Ising’s surmise was wrong.
A population of theorists floating uneasily between physics and materials science (but a number of them working in materials science departments) have become specialists in the statistical thermodynamics of solids, critical phenomena in particular, working in specific fields such as order-disorder transitions; to go into any details of critical phenomena here would take us much too far into the domain of mathematical physics. Two splendid historical accounts of the whole field are by Domb (1995, 1996); another important historical treatment is by Brush (1967). It is intriguing that Ising’s name was immortalised in the Ising Model, but in Domb’s opinion (private communication), "Ising was a low-grade scientist who by a quirk of fate managed to get his name on thousands of papers, many of them outstandingly good. 3. _________
From the historical point of view, an interesting dispute concerns the relative claims of Maxwell in England, Josiah Willard Gibbs in America and Ludwig Boltzmann in Austria to be regarded as the true father of statistical thermodynamics - as distinct from macroscopic chemical thermodynamics, where Gibbs’ claims are undisputed. Gibbs’ claim rests on a book in 1902 (Gibbs 1902), but this is a good deal later than the various classic papers by Boltzmann. The most important of these were his study of the process by which a gas, initially out of equilibrium, approaches the Maxwell Boltzmann distribution (as it has since become known), and his profound investigation in 1877 of the probabilistic basis of entropy, culminating in the relation S = k log W, where S is entropy and W is the probability of a microstate; this immortal equation is carved on Boltzmann’s tomb. 4. _________
The sequence of events is traced with historical precision in a new biography of Boltzmann (Cercignani 1998). 5. _________ Cercignani attributes this to the unfamiliarity of many physicists early in this century with Boltzmann’s papers, partly because of the obscurity of his German style (but Gibbs is not easy to read, either!), and partly because the great opinion-formers of early 20th-century physics, Bohr and Einstein, knew little of Boltzmann’s work and were inclined to decry it. The circumstances exemplify how difficult it can be to allocate credit appropriately in the history of science.
| Task 4. | Match the words in column A with their Ukrainian equivalents from column B: | ||||
| A | B | ||||
| statistical thermodynamics | a) | ||||
| quirk of fate | b) | ||||
| mutually colliding molecules | c) | ||||
| to allocate | d) | ||||
| to apply | e) | ||||
| electromagnetic equation | f) | ||||
| to exemplify | g) | ||||
| chaotic assembly of molecules | h) | ||||
| to attribute | i) | ||||
| order-disorder transition | j) | ||||
| to carve | k) | ||||
| probabilistic analysis | l) | ||||
| spin alignment | m) | ||||
| crystalline solid | n) | ďĺđĺěłůĺíí˙ âďîđ˙äęîâŕíłńňü-íĺâďîđ˙äęîâŕíłńňü | |||
| Task 5. | Give the Ukrainian equivalents to the following words and word combinations: |
crystalline solids, pressure-volume-temperature relationship, electromagnetic equations, interestingly applicable to, spin alignment, order-disorder transitions, splendid historical accounts, to be negligible, macroscopic chemical thermodynamics, initially out of equilibrium, profound investigation, unfamiliarity, obscurity of style, to exemplify.
| Task 6. | Answer the following questions: |
| 1. Who was the founder of the kinetic theory of gases? |
| 2. What were the first steps in forming kinetic theory of gases? |
| 3. Who described order-disorder transitions and how can we name such phenomena? |
| 4. What did Rudolf Peierls make in the field of critical phenomena? |
| 5. Who became specialists in the statistical thermodynamics of solids? |
| 6. Is “Ising Model” the correct name for the treatment? |
| 7. What is carved on Boltzmann’s tomb? |
| 8. What is Gibb’s book about? |
FOR THE FULFILL THE OVERALL OBJECTIVE STUDENT SHOULD BE ABLE
| specific objectives | Purpose of the initial level of knowledge |
| 1. Know the algorithm for the examination of the patient in clinical prosthodontics. | 1. To be able to conduct the clinical examination of the patient, the diagnosis, the chosen design. |
| 2. Know the sequence of stages of examination of patients in clinical prosthodontics. | 2. To be able to conduct the first stage of examination of patients: survey and record the data in the patient card dental patient (form 043/0). |
| 3. Know the structure of the upper and lower jaw. | 3. To be able to determine the relationship of the upper and lower jaw. |
| 4. Know the structure of the oral mucosa. | 4. To be able to determine the presence of clinically submucosal layer in different parts of the oral mucosa. |
| 5. To be able to formulate a diagnosis and to complete ambulatory medical record. | 5. Know the structure of the diagnosis and the types of medical records, which is used in prosthetic dentistry clinic |
Theoretical questions ON WHICH BASIS PERFORMANCE OF TARGET KINDS OF ACTIVITY IS POSSIBLE
- Especially examination of patients with edentulous jaws
- Anatomical and functional feature oral cavity of patients with edentulous jaws.
- Changes in the upper and lower jaws by account of full loss of teeth.
- Definition of term “diagnosis” in orthopedic dentistry. Structure and components of diagnosis.
- Medical history. Rules of records. Formulation of the diagnosis (parts of diagnosis and substantiation).
SRWS (studying and research work of the student)
Write and sketch:
- Classification of the atrophy edentulous upper jaw by Shreder.
- Classification of the atrophy edentulous lower jaw by Keller.
- Classifications of conditional of the mucous membrane edentulous jaws by Lund and Supple.
- Determination pliancy of mucous membrane of hard palatal and alveolar processes.
PRACTICAL SKILLS:
- Anamnesis: determination and structures.
- Extraoral examination: essence.
- Intraoral examination of patients with edentulous jaws.
- Methods of preparation oral cavity for manufacturing complete dentures.
Date: 2015-01-02; view: 1888
| <== previous page | | | next page ==> |
| Concept of algorithm. | | | Literature recommended |