Approximation of Constant Evaporation After a Set Point

In order to produce a solid film via spin coating, the solution must evaporate. At the start the concentration of the solute is uniform. The solvent evaporates uniformly over the entire surface area causing a solids concentration c(t) to increase, independently of r since h is independent of r for uniform films. Making the additional approximations i) that c is independent of z, ii) that the volume of the liquid solution is equal to the volume of the solvent plus the volume of the solute, and iii) that the evaporation rate is only a function of experimental parameters such as spin speed, one may define a volume per unit area L of liquid and S of solid, so that c(t)=S/(S+L) and h(t)=S+L. The initial film thickness will reduce uniformly as before, but the thinning rate is different. The rate of change of S and L due to outflow and evaporation at rate e is [7]

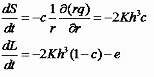
These are rates of change of volume per unit area and in theory they can be integrated from initial thickness and concentration values until L=0 and only the solid film remains. However, they cannot be solved analytically.

Meyerhofer solves them numerically, with an empirical relationship between viscosity and concentration of β=β_solvent+β_solids*c^γ, with γ around 2.5 for photoresists. [7] He determines that, if the spin speed is fast enough that the final film thickness does not depend on the initial solution thickness but only on the spin speed - fast enough to generate an outflow-dominated stage that diminishes S₀ by 50% or more - then a reasonable approximate solution may be obtained by dividing the spin coating process into two stages. (Fig. 2, c and d) In the first, viscous forces predominantly determine the film thickness. In the second, the film has become thin enough and dense enough that fluid flow essentially stops, and from that point on solvent evaporation dominates. The transition, when the evaporation rate and the viscous flow rate become equal, may be considered the point at which the film "sets" or gels on the substrate. So the initial stage proceeds until the evaporation and outflow contributions are equal:

with c~c₀ and β~β₀ since up to this point the solution concentration has been constant. Beyond this point, outflow is negligible, and

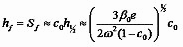
Especially for initially thick films and higher spin speeds, this result is a very good approximation to the numerical solution of the full equations with identical parameters.

Viscosity is a particular function of the material being spin coated; however e is not a constant but is proportional to the rate of airflow over the surface, which in turn is (most simply) proportional to the square root of the spin speed. [9] With this in mind,

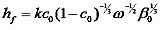
with a proportionality constant dependent on the system airflow that must be measured for a given spin coater. The dependence of the final film thickness on the inverse square root of the spin speed is the most common reported experimental relationship between these two quantities, [10] so for simple systems experiment and theory are already in agreement.

Bornside et. al. in 1991 [10] modify this analysis slightly, to eliminate the empirical constants in the equation. They set the rate of evaporation as

where k is the mass transfer coefficient, x_A⁰ is the initial concentration of solvent in the coating liquid, and x_A^∞ is the mass fraction of solvent in the coating liquid that would be in equilibrium with the mass fraction of solvent in the bulk gas. Then the thickness of the wet film when outflow ceases is

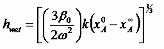
and the thickness of the dry film with no liquid that remains at the end of the process is

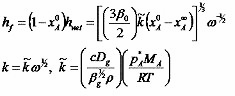
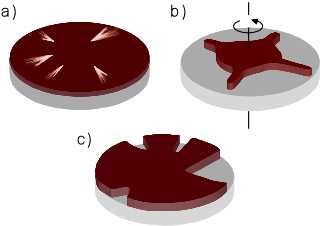
Fig. 3: Deviations from the ideal spin coated film. a) Streaks in the film, probably due to particulate matter on the substrate. b) Nonuniform liquid expansion during spinning, due mainly to imperfect substrate wetting. c) Areas of the substrate remain uncoated, which occurs often if the initial liquid volume is too small.

with the dependence on ω pulled out explicitly. c depends on the Schmidt number (the ratio of kinematic viscosity and mass diffusivity) of the ambient gas, D_g is the binary diffusivity of the solvent in the ambient gas, β_g is the kinematic viscosity of the ambient gas, p_A^* is the vapor pressure of the pure solvent at temperature T, and M_A is the molecular weight of the solvent. [10] Bornside et. al. derive this relation from the mass transfer coefficient for transport from the surface of an infinite spinning disk to the bulk of a semi-infinite fluid in laminar flow above it, [11-13] coupled with the relation between vapor pressure and mole fraction in an ideal solution. [14] They compare this result to experimental data obtained using spin coated poly(methyl methacrylate) dissolved in chloroform, and obtain reasonable agreement with their theoretical results.

Date: 2014-12-29; view: 1010