Approximation of No Evaporation

Ignoring evaporation completely, the basic physics were first worked out by Emslie et. al. [8] By making all of the assumptions described in the previous section, and equating the viscous and centrifugal forces per unit volume, you get

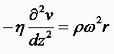
where η is the viscosity, ρ the liquid density, ω the spin speed, and v the radial velocity at any point (r, θ, z). For convenience, β=η/ρ defines the kinematic viscosity. Integrating with the boundary conditions that v=0 at the disk surface of z=0, and that dv/dz=0 at the free surface where there cannot be a shearing force, gives

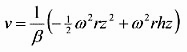
From v, radial flow q is easily obtained by integration over z. h is the film thickness. Combining this with continuity equation

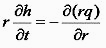
gives the differential equation which governs the thickness of the liquid film on the surface as a function of time:

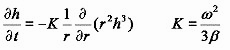
As a check, for a uniform initial liquid distribution (h independent of r), the final liquid distribution is also uniform, and a thick layer thins significantly faster than a thin one so there will be a tendency towards uniformity for nonuniform initial films.

Using this last equation and the total derivative expression

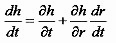
one may write

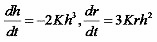
with solutions

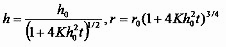
These solutions give the coordinates (r, h) of any point on the surface of the disk, in terms of original coordinates (r₀, h₀). Emslie et. al. analyze the problem further by considering the time and radius dependence of several different initial fluid distributions, and find increasing uniformity with increasing centrifugation time, within the range of validity of the initial set of assumptions. Of course, since there is an infinite disk and no solution evaporation to thicken and solidify the liquid, it will continue to flow radially outwards and thin for ever.

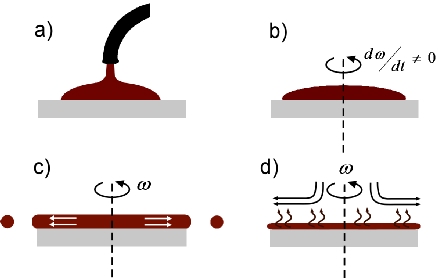
Figure 2: The different "stages" of spin coating. a) Dispensation (not modeled). b) Acceleration (not modeled). c) Flow dominated. d) Evaporation dominated.

Date: 2014-12-29; view: 1000