Parallel to the axis ОУ.

Coincides with the axis ОУ.

Passes through the origin coordinates.

Вопрос № 74

How is located the straight Ах+Ву+С=0, if A=C=0:

coincides with the axis ОХ.

Parallel to the axis ОУ.

Parallel to the axis ОХ.

Coincides with the axis ОУ.

Passes through the origin coordinates.

Вопрос № 75

How is located the straight Ах+Ву+С=0, if B=C=0:

Coincides with the axis ОУ.

Coincides with the axis ОХ.

Parallel to the axis ОУ.

Parallel to the axis ОХ.

Passes through the origin coordinates.

Вопрос № 76

Transpose is the matrix when:

permutation rows and columns.

permutation two rows.

permutation two columns.

Multiplication of all the matrix elements on the number.

Summation two matrixes.

Вопрос № 77

Sho the formula derivative function y=arccosx:

Вопрос № 78

Product of matrixes А*Е equals:

A.

E.

–A.

–E.

A².

Вопрос № 79

Compute and determine the 3rd order:

-12.

12.

0.

10.

-10.

Вопрос № 80

Find the matrix Х, that satisfy the fellow conditions: 2А+Х=В where: А= В=

Вопрос № 81

Coordinate of the point М (х; у), divides the segment АВ with endpoints A(х₁; у₁) and B(х₂; у₂) on .

.

у-у₁=k(х-х₁).

.

.

.

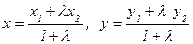Вопрос № 82

Area of a triangle with vertices, А(-2; -4) , В(2; 8), С(10; 2) :

60 square units.

50 sq. un.

40 sq. un.

30 sq. un.

20 sq. un.

Вопрос № 83

Expression of the polar coordinates of the point M in rectangular coordinates:

.

.

.

Вопрос № 84

Expression of the polar coordinates of the point M in rectangular coordinates:

.

.

.

Вопрос № 85

The general equation of second degree:

Ax²+Bхy+Cу²=+Dx+Ey+F=0.

Ax+By+C=0.

у=kx+b.

Вопрос № 86

The equation of a circumference with center at point C (a; b) and radius r:

(х-а)²+(у-b)²=r².

Ax+By+C=0.

у=kx+b.

Вопрос № 87

The equation of a circumference with center at point C (0, 0) and radius r:

х²+у²=r².

у=kx+b.

(х-а)²+(у-b)²=r².

Вопрос № 88

The equation of the circumference if center of the circle coincides with the origin coordinates:

х²+у²=r².

у=kx+b.

(х-а)²+(у-b)²=r².

Вопрос № 89

The equation of a circumference with center at C (2, -4) and radius 5:

(х-2)²+(у+4)²=25.

х²+у²=25.

у=kx+b.

(х-а)²+(у-b)²=r².

Вопрос № 90

The equation of a circumference centered at point C (0, 0) and a radius of 4:

х²+у²=16.

у=kx+b.

(х-а)²+(у-b)²=r².

Вопрос № 91

Compute and determine the 2^nd order:

-2.

10.

-10.

2.

0.

Вопрос № 92

Compute and determine the 2nd order:

8.

-8.

-120.

0.

1.

Вопрос № 93

Compute an determine the 3^rd order:

29.

-29.

27.

20.

2.

Вопрос № 94

Compute and determine the 3rd order:

0.

1.

-1.

2.

-2.

Вопрос № 95

Find the sum of the matrixes и

0.

Вопрос № 96

Compute the multiplication of the matrixes АВ, if А= В=

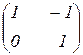
Вопрос № 97

Find matrix А+2В, if А= В=

Вопрос № 98

Find matrix 3А-В, if А= В=

Вопрос № 99

Find matrix А+2В, if А= В=

Вопрос № 100

Compute the multiplication of the matrix АВ, if А= В=

Вопрос № 101

Solve the system of equalization:

(-7; 5).

(-7; -5).

(7; 0).

(5; 7).

(0; 1).

Вопрос № 102

Compute and determine the 3rd order:

0.

1.

-1.

-2.

2.

Вопрос № 103

Compute and determine the 3rd order:

1.

0.

-1.

3.

-3.

Вопрос № 104

Compute and determine the 2rd order:

2.

-1.

1.

0.

-2.

Вопрос № 105

Compute and determine the 2rd order:

1.

-9.

9.

-1.

0.

Вопрос № 106

Compute the multiplication of the matrixes АВ, if А= В=

Вопрос № 107

Compute the multiplication of the matrixes АВ, if А= В=

Вопрос № 108

Find matrix А+В, if А= В=

Вопрос № 109

Find matrix А-В, if А= В=

Вопрос № 110

Compute and determine the 3^rd order:

-5.

-1.

5.

1.

0.

Вопрос № 111

If А= В= 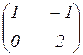, then matrix С=2А+В has a form:

Вопрос № 112

if (х₀, у₀)- the solution of system linear equalization ,

then х₀ - у₀ equal:

-7,5.

0,5.

7,5.

-0,5.

0.

Вопрос № 113

Find which the identity matrix is:

Е= .

Е= .

Е= .

Е= .

Е= .

Вопрос № 114

Matrix size:

(3x3).

(4x3).

(3x4).

(3x2).

(2x3).

Вопрос № 115

Operations on matrices:

addition, multiplication by the number, the product.

addition, multiplication by the number.

multiplication by the number, the product.

the product.

addition.

Вопрос № 116

Determine the order of the determinant:

2-order.

1-order.

4-order

6-order

n-order.

Вопрос № 117

Square matrix:

Вопрос № 118

Calculate determine the 3rd order:

0.

2.

6.

5.

-1.

Вопрос № 119

Find the product matrix on the number of: 4

Вопрос № 120

Search matrix А*В: А= В=

0.

2.

-1.

1.

5.

Вопрос № 121

Search matrix *A если =5 А=

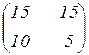
Вопрос № 122

Calculate determine the 3rd order:

0.

-2.

5.

-10.

10.

Вопрос № 123

Calculate determine the 3rd order:

0.

-12.

-10.

10.

-1.

Вопрос № 124

Calculate determine the 3rd order:

0.

64.

-64.

-1.

1.

Вопрос № 125

Search matrix А+В if А= В= ,

Вопрос № 126

Formula Cramer:

.

.

.

.

.

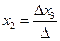
Вопрос № 127

Calculate determine the 2-th order:

1.

-1.

0.

2.

-2.

Вопрос № 128

Determine the order of the determinant:

n-order.

1-order.

2-order.

3-order.

4-order.

Вопрос № 129

To multiply matrix the number

Each element of the matrix multiplied by the number of

Each element of the first row of the matrix multiplied by the number of

Each element of the first column of the matrix multiplied by the number .

Each element of the second column of the matrix multiplied by the number of .

Each element of the column and row of the matrix multiplied by the number .

Вопрос № 130

Calculate the determinant of the matrix

-1

-50

Вопрос № 131

Dimension of matrices:

mxn.

mxm.

nxn.

nx1.

m=1.

Вопрос № 132

The order of the determinant, consisting of n-elements:

3-порядка.

n –порядка.

4-порядка.

6-порядка.

5-порядка.

Вопрос № 133

An additional determinant of the system:

Вопрос № 134

If you multiply this matrix by a unit matrix, we obtain:

this matrix.

identity matrix.

zero matrix.

square matrix.

inverse matrix.

Вопрос № 135

Formula for calculating the determinant of second order:

.

.

.

.

.

Вопрос № 136

If the items are below the main diagonal are zero, then the square matrix is called:

triangular.

diagonal.

unit and square.

square.

unit.

Вопрос № 137

An additional determinant of the system:

Вопрос № 138

Methods for solving systems of linear equations:

Kramer, Gauss-Jordan.

Sarryusa and Kronecker - Capelli.

Cauchy problem.

Sarryusa.

Kronecker - Capelli.

Вопрос № 139

B as a matrix of four laboratory feeding birds in two different types of food:

Вопрос № 140

Short name of the matrix:

.

.

.

.

.

Вопрос № 141

Elements of the matrix form:

columns and rows.

lines and diagonals.

diagonal.

columns.

line.

Вопрос № 142

Matrix called:

vector - a string.

vector - column.

vector - a line and vector - the column.

the diagonal.

vector.

Вопрос № 143

Matrix called:

vector - column.

vector - a string.

vector - a line and vector - the column.

the diagonal.

vector.

Вопрос № 144

Key containing two identical columns:

is zero.

is 1.

is equal to -1.

is 12.

is 15.

Вопрос № 145

Additional determinant of the system:

Вопрос № 146

Key to containing two proportional columns:

is zero.

equal to -2.

is 1.

equal to -5.

is 5.

Вопрос № 147

If one of the rows of the determinant consists of zeros, the determinant:

is zero.

is -1.

is 1.

is 5.

is equal to -6.

Вопрос № 148

Determination of the identity matrix:

diagonal elements are composed of units of the remaining zeros.

elements of the first line consists of all ones.

elementy first column consist of all ones.

all elements are equal to unity.

matrix consisting of one row or one column.

Вопрос № 149

What condition is required to add two matrices:

the same dimension matrices.

the various dimensions of matrices.

the number of rows of the first matrix equals the number of columns of the second matrix.

the number of columns of the first matrix equals the number of rows of the second matrix.

diagonal elements are the same.

Вопрос № 150

What condition must be fulfilled for the multiplication of two matrices:

number of columns of the first matrix equals the number of rows of the second matrix.

the same diagonal elements.

the same dimensions.

the number of columns are equal.

the number of rows are equal.

Вопрос № 151

In which case the system of equations is called homogeneous:

all the free terms are equal to zero.

free terms different numbers.

at least one of the free terms equal to zero.

at least one of the free terms equal to unity.

all free members are equal to unity.

Вопрос № 152

Find a matrix A*B if

Вопрос № 153

Find a matrix A*B if

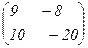
Вопрос № 154

Solve the system of equations:

(2;-5).

(1;6).

(8;1).

(-5;2).

(1;0).

Вопрос № 155

Calculate to determine the 2-nd order:

(a+b)(c+k)-(b+k)(a+c).

(a+k)(c-b).

ck+ab.

ab.

ac.

Вопрос № 156

Calculate to determine the 2-nd order:

0.

-18.

2.

4.

5.

Вопрос № 157

Calculate the determinant of the matrix:

44.

18.

0.

52.

16.

Вопрос № 158

Calculate the determinant of the matrix:

50.

16.

-50.

70.

0.

Вопрос № 159

Calculate the determinant of the matrix:

-1.

0.

50.

16.

-50.

Вопрос № 160

Find a matrix * A if =3

Вопрос № 161

Calculate determine the 3rd order:

40.

1.

65.

0.

-40.

Вопрос № 162

Calculate determine the 3rd order:

-5.

5.

1.

0.

10.

Вопрос № 163

Calculate determine the 3rd order:

16.

8.

1.

48.

17.

Вопрос № 164

Solve the system of equations:

(5;-1).

(0;1).

(-1;5).

(1;1).

(8;3).

Вопрос № 165

Solve the system of equations:

(1;1;1).

(1;1;-1).

(1;0;1).

(-1;1;-1).

(1;2;1).

Вопрос № 166

Solve the system of equations:

(-3;2;-1).

(-3;2;0).

(-3;6;-1).

(-3;4;-1).

(3;2;1).

Вопрос № 167

Solve the system of equations:

(-1;-2;4).

(-1;0;3).

(-1;-9;4).

(-1;-5;4).

(0;-2;4).

Вопрос № 168

Solve the system of equations:

(1;2;3).

(-1;2;3).

(1;2;-3).

(1;5;3).

(1;2;0).

Вопрос № 169

If the matrix , then the matrix 3A is:

Вопрос № 170

If the matrix , then the matrix 5A is:

Вопрос № 171

Matrix product * is:

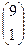
Вопрос № 172

Calculate the determinant :

2.

-1.

1.

5 .

6.

Вопрос № 173

Calculate the determinant :

6.

-6.

5.

2.

3.

Вопрос № 174

Calculate the determinant :

2.

-2.

3.

1.

-1.

Вопрос № 175

Calculate the determinant :

6.

-2.

3.

1.

-1.

Вопрос № 176

In which case the determinant does not change

if interchange rows and columns with the same number

if you rearrange the columns

if you multiply the determinant to zero

if you rearrange the rows and columns with different numbers

if you multiply the determinant by one

Вопрос № 177

An additional determinant of :

is obtained by substituting the second column of free terms.

obtained by substituting the first column of free terms.

obtained by substituting the third column of free terms.

obtained by multiplying the determinant to zero.

obtained by multiplying the determinant of one.

Вопрос № 178

What is the number of rows of the matrix?

m=1.

n=0.

m=0.

m=n.

n=1.

Вопрос № 179

If the determinant of the system is different from zero, then the solution of the system:

is unique.

x=0 y=0.

no solutions

y=0.5

non solution

Вопрос № 180

Elements the main diagonal:

А₁₁А₂₂А₃₃

А₃₃А₂₃ А₁₁

А₃₂А₂₃ А₂₁

А₂₁А₃₂А₃₃

А₃₂А₂₃ А_{11 .}

Вопрос № 181

An additional determinant of the system

Вопрос № 182

Solution of the system are:

x₁=1, x₂=-2.

x₁=-1, x₂=2.

x₁=-2, x₂=1.

x₁=-1, x₂=0.

x₁=1, x₂=0.

Вопрос № 183

Solution of the system are:

x₁=3, x₂=-1.

x₁=-1, x₂=3.

x₁=1, x₂=3.

x₁=-3, x₂=1.

x₁=-1, x₂=2.

Вопрос № 184

Solution of the system are:

x₁=2, x₂=-3.

x₁=-2, x₂=3.

x₁=-3, x₂=2.

x₁=-3, x₂=1.

x₁=3, x₂=0.

Вопрос № 185

Solution of the system are:

x₁=3, x₂=-5.

x₁=-5, x₂=2.

x₁=-5, x₂=-3.

x₁=5, x₂=-3.

x₁=-3, x₂=5.

Вопрос № 186

Solution of the system are:

No solution.

(-8;4;3).

(8;-4;3).

(-2;1;0).

(-2;-1;0).

Вопрос № 187

Solution of the system are:

(-1;1;0).

No solution.

(-8;4;3)

(8;-4;3).

(-2;-1;0).

Вопрос № 188

Solution of the system are:

(2;2;2).

(-2;2;1).

No solution.

(-2;1;0).

(-2;2;0).

Вопрос № 189

Solution of the system are:

(4;3;2;0).

No solution.

(-2;3;2;3).

(0;2;1;3).

(-2;2;0;1).

Вопрос № 190

A square matrix A n-th order is called degenerate if:

detA=0.

detA 0.

detA=1.

detA=-1.

detA=A^*/A^-1.

Вопрос № 191

The sum of matrices A + B, if , equal to:

Вопрос № 192

Disposition of straight Ах+Ву+С=0, if В=0, С 0:

parallel to axis ОХ;

axis ОХ;

parallel to axis ОУ;

axis ОУ;

passes through the origin coordinates.

Вопрос № 193

Angular coefficient of the straight 2,5у-5х+5=0:

2;

2,5;

-2;

-2,5;

5;

Вопрос № 194

Disposition of stright Ах+Ву+С=0, если А=0, С 0:

parallel to axis ОХ;

axis ОХ;

parallel to axis ОУ;

axis ОУ;

passes through the origin coordinates;

Вопрос № 195

А(2; -3) and В(4;3). Coordinates of the point, divides the interval АВ in two:

(3;0).

(2; -3).

(4; 3).

(-2; 3).

(6; -3).

Вопрос № 196

Equalization of parabola, that symmetrical relative to the axis coordinates:

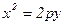
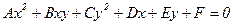
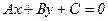
Вопрос № 197

Equalization of parabola, symmetrical relatively to axis of abscissas:

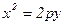
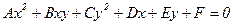
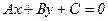
Вопрос № 198

Equalization of parabola directrix:

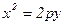
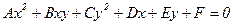
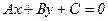
Вопрос № 199

Size of р parabola is calling:

Parameter.

Ordinate.

Abscissa.

Focus.

Directrix.

Вопрос № 200

Coordinates of focus F parabola:

и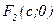

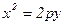
Date: 2015-12-11; view: 1107