
CATEGORIES:
BiologyChemistryConstructionCultureEcologyEconomyElectronicsFinanceGeographyHistoryInformaticsLawMathematicsMechanicsMedicineOtherPedagogyPhilosophyPhysicsPolicyPsychologySociologySportTourism
Parallel to axis ÎÕ.
Âîïðîñ ¹ 9
Solve the system if equations: 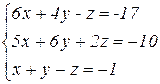
(-4; 2; -1).
(4; -2; 1).
(4; -1; 2).
(0; 2; 1).
(-1; 2; 0).
Âîïðîñ ¹ 10
Compute and determine the 2nd order: 
17.
-18.
0.
10.
-10.
Âîïðîñ ¹ 11
The equation of a circumference of radius R = 5 with center at the origin:
õ2+ó2=25.
õ2+ó2=16.
ó=kx+b.
(õ-à)2+(ó-b)2=r2.

Âîïðîñ ¹ 12
The equation of a circumference of radius R = 7 with the coordinates of the center: the abscissa a = 3, the ordinate b=-2:
(õ-3)2+(ó+2)2=49.
õ2+ó2=16.
ó=kx+b.
(õ-à)2+(ó-b)2=r2.
õ2+ó2=25.
Âîïðîñ ¹ 13
The point of intersection of the circumference (õ-4)2+ó2=25:
Ì(0;  3)
3)
Ì(-2; -4).
Ì(-2; -4).
Ì(0; -4).
Ì(0; 0).
Âîïðîñ ¹ 14
Coordinates of a center and radius R of the circumference (õ-2)2+(ó+4)2=25:
Î(2;-4); R=5.
Î(0; 0); R=5.
Î(2;-4); R=25.
Î(2;4); R=25.
Î(-2;4); R=5.
Âîïðîñ ¹ 15
Coordinates of a center and radius of the circumference õ2+ó2-25=0:
Î(0; 0); R=5.
Î(2;-4); R=5.
Î(2;-4); R=25.
Î(2;4); R=25.
Î(-2;4); R=5.
Âîïðîñ ¹ 16
Show the equation of circumference, where the center is situated in point (2;-3) and circumference passes through the point (5;1):
(õ-2)2+(ó+3)2=25.
õ2+ó2=16.
ó=kx+b.
(õ-à)2+(ó-b)2=r2.
(õ-3)2+(ó+2)2=49.
Âîïðîñ ¹ 17
The distance between centers of the circumferences õ2+ó2=16 and (õ+3)2+(ó+4)2=25:
5.
4.
3.
25.
16.
Âîïðîñ ¹ 18
Abscissa of the circumference’s point õ2+(ó+4)2=41 and the point on it with ordinate equals zero:
5.
4.
3.
25.
16.
Âîïðîñ ¹ 19
The curve, specified by equalization (õ-à)2+(ó-b)2=r2:
Circumference.
Parabola.
Ellipse.
Hyperbola.
Straight line.
Âîïðîñ ¹ 20
Ordinate of the circumference’s point (õ+3)2+ó2=25, where abscissa equals zero:
4.
5.
3.
25.
16.
Âîïðîñ ¹ 21
A canonical equalization of the ellipse:

(õ-à)2+(ó-b)2=r2.
ó=kx+b.
õ2+ó2=16.

Âîïðîñ ¹ 22
The curve, set by the equalization  :
:
Ellipse.
Circumference.
Parabola.
Hyperbola.
Straight line.
Âîïðîñ ¹ 23
The point of intersection the hyperbola õ2-4ó2=16 with the axis of abscissas:
Ì( ±4; 0).
Ì( -5; 1).
Ì( ±5; 0).
Ì( ±6; 0).
Ì( ±7; 0).
Âîïðîñ ¹ 24
Coordinates the point Ì, hyperbola õ2-9ó2=16 with the ordinate, equals 1:
Ì( ±5; 1).
Ì( ±4; 0).
Ì( ±5; 5).
Ì( 0; 0).
Ì( ±5; 25).
Âîïðîñ ¹ 25
Canonical type of hyperbola 64õ2-25ó2=1600:




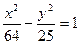
Âîïðîñ ¹ 26
Canonical type of the ellipse 9õ2+25ó2=225:
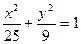



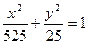
Âîïðîñ ¹ 27
Equalizations of asymptotes of the hyperbola  :
:

 , c>a.
, c>a.
 , c<a.
, c<a.
 .
.
 .
.
Âîïðîñ ¹ 28
Equalizations of asymptotes of the hyperbola  :
:
 .
.
 .
.
 , c<a.
, c<a.
 , c<a.
, c<a.
 .
.
Âîïðîñ ¹ 29
Describe the distance d from origin coordinates to point Ì(õ;ó):
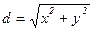 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Âîïðîñ ¹ 30
The distance d from origin coordinates to point Ì(-3; 4):
5;
25;
1;
-7;
-12;
Âîïðîñ ¹ 31
The distance between two points Ì1(õ1;ó1)è Ì2(õ2;ó2):





Âîïðîñ ¹ 32
The distance between two points Ì1(8; 3)è Ì2(0; -3):
10.
0.
11.
100.
-11.
Âîïðîñ ¹ 33
Length of the cutoff ÀÂ with the coordinates À(õ1;ó1) and Â(õ2;ó2):





Âîïðîñ ¹ 34
Length of the cutoff ÀÂ with the coordinates À(2; 4)è Â(5;8):
5;
25;
1;
-7;
-12;
Âîïðîñ ¹ 35
A triangle set by the coordinates of its apices À(1; 1), Â(4;1), Ñ(1;5). Length of the side ÀÂ equals:
3;
25;
1;
-7;
-12;
Âîïðîñ ¹ 36
Coordinates of the interval’s midpoint ÀÂ, À(õ1;ó1)and Â(õ2;ó2):
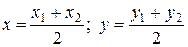 .
.
 .
.
 .
.
 .
.
 .
.
Âîïðîñ ¹ 37
Coordinates of the interval’s midpoint ÀÂ, À(1;-1)è Â(5;9):
(3; 4).
(1;-1).
(5; 9).
(3; 4).
(6; 8).
Âîïðîñ ¹ 38
A rectangle prescribed by coordinates of its apices À(1; 1), Â(3;1), Ñ(1;5). Coordinates of the eg’s midpoint ÀÑ:
Ì(2; 1), N(2;3), P(1;3).
Ì(1; 1), N(2;3), P(1;5).
Ì(2; 2), N(3;3), P(1;3).
Ì(1; 1), N(2;3), P(1;3).
Ì(2; 1), N(3;1), P(1;5).
Âîïðîñ ¹ 39
A rectangle prescribed by coordinates of its apices À(1; 1), Â(8;-5), Ñ(3;5).Point Ì the midpoint of the leg ÀÑ. Length of the median ÂÌ equals:
10;
6;
7;
8;
9;
Âîïðîñ ¹ 40
Disposition of straight Àõ+Âó+Ñ=0, if Â=0, Ñ  0:
0:
parallel to axis ÎÕ;
axis ÎÕ;
parallel to axis ÎÓ;
axis ÎÓ;
passes through the origin coordinates.
Âîïðîñ ¹ 41
Angular coefficient of the straight 2,5ó-5õ+5=0:
2;
2,5;
-2;
-2,5;
5;
Âîïðîñ ¹ 42
Disposition of stright Àõ+Âó+Ñ=0, åñëè À=0, Ñ  0:
0:
parallel to axis ÎÕ;
axis ÎÕ;
parallel to axis ÎÓ;
axis ÎÓ;
passes through the origin coordinates;
Âîïðîñ ¹ 43
À(2; -3) and Â(4;3). Coordinates of the point, divides the interval ÀÂ in two:
(3;0).
(2; -3).
(4; 3).
(-2; 3).
(6; -3).
Âîïðîñ ¹ 44
Equalization of parabola, that symmetrical relative to the axis coordinates:


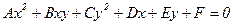
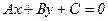

Âîïðîñ ¹ 45
Equalization of parabola, symmetrical relatively to axis of abscissas:

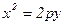
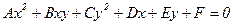
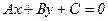

Âîïðîñ ¹ 46
Equalization of parabola directrix:

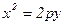

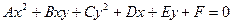
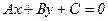
Âîïðîñ ¹ 47
Size of ð parabola is calling:
Parameter.
Ordinate.
Abscissa.
Focus.
Directrix.
Âîïðîñ ¹ 48
Coordinates of focus F parabola:

 è
è 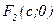

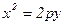

Âîïðîñ ¹ 49
Coordinates of focus F parabola  :
:



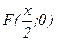

Âîïðîñ ¹ 50
Equalization of directrix parabola  :
:



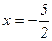

Âîïðîñ ¹ 51
Canonical equalization of hyperbola, where à=5, â=8:

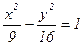
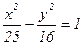


Âîïðîñ ¹ 52
Canonical equalization of ellipse, if à=7, b=5:





Âîïðîñ ¹ 53
Canonical equalization, and distance between the focuses equal 8 and small axle b=3:





Âîïðîñ ¹ 54
Canonical equalization of ellipse, where large axle à=6 , concentricity. 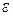 =0,5:
=0,5:





Âîïðîñ ¹ 55
What the dimension of matrix Ñ=ÀÂ, if À(m x k), Â(k x n):
(m x n).
(k x n).
(n x m).
(m x k).
(n x n).
Âîïðîñ ¹ 56
What the dimension of matrix Ñ=ÀÂ, if À(2 x 3), Â(3 x 4):
(2 x 4).
(2 x 3).
(2 x 2).
(3 x 4).
(4 x 3).
Âîïðîñ ¹ 57
What the dimension of matrix Ñ=ÀÂ, if À(3 x 4), Â(4 x 1):
(3 x 1).
(3 x 4).
(4 x 4).
(3 x 3).
(1 x 3).
Âîïðîñ ¹ 58
What the dimension of matrix Ñ=ÀÂ, if À(2 x 4), Â(4 x 2):
(2 x 2).
(4 x 2).
(2 x 8).
(2 x 4).
(4 x 4).
Âîïðîñ ¹ 59
Find an element Ñ23 matrix Ñ=ÀÂ, if  ,
,  :
:
10.
5.
-10.
-5.
-9.
Âîïðîñ ¹ 60
Find an element Ñ12 matrix Ñ=ÀÂ, if  ,
,  :
:
-5.
5 .
10.
-10.
-9.
Âîïðîñ ¹ 61
Find an element Ñ33 matrix Ñ=ÀÂ, if  ,
,  :
:
2.
-5.
-10.
10.
5.
Âîïðîñ ¹ 62
If the determiner square matrix equals zero, she called:
Singular.
Nonsingular.
Unit.
Inverse.
Diagonal.
Âîïðîñ ¹ 63
If the determiner if square matrix is not equal zero, she called:
Singular.
Nonsingular.
Unit.
Inverse.
Diagonal.
Âîïðîñ ¹ 64
The system of linear equalizations is calling compatible, if:
it has only one solution.
it has at least one solution.
It doesn’t have a solution.
The solutions consist from the whole numbers.
The solutions only positive numbers.
Âîïðîñ ¹ 65
n – unknown quantity, m – quantity of the equalization of the system. What kind of condition contribute application the Kramer’s rule?
m = n.
m £ n.
m ³ n .
m < n.
m > n.
Âîïðîñ ¹ 66
Coordinates of focus F parabola  :
:



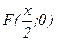

Âîïðîñ ¹ 67
If the equalization’ system doesn’t have solution, then the system is calling:
Incompatible .
Compatible.
Determinate.
Heterogeneous.
Homogeneous.
Âîïðîñ ¹ 68
If in the Kramer’s method D=0, Dõ¹0, then a system:
Incompatible .
Compatible.
Determinate.
Heterogeneous.
Homogeneous.
Âîïðîñ ¹ 69
How is located the straight Àõ+Âó+Ñ=0, if Â=0, ѹ0:
Parallel to axis ÎÓ.
Axis ÎÕ.
Parallel to axis ÎÕ.
Axis ÎÓ.
Passes through the origin coordinates.
Âîïðîñ ¹ 70
Formula of the calculus of the distance from point Ì(õ1,ó1) to the straight Àõ+Âó+Ñ=0:



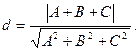

Âîïðîñ ¹ 71
In what meanings à and â these straights àõ-2ó-1=0, 6õ-4ó-â=0 are parallel:
à=3, â  2.
2.
à=2, â=2.
à=3, â=2.
à= -3, â  2.
2.
à=6, â  6.
6.
Âîïðîñ ¹ 72
In what meanings à and â these straights ó = àõ+2, ó = 5õ - â are parallel:
à= 5, â  -2.
-2.
à= -1/5, â  -2.
-2.
à= -1/5, â= -2.
à= -5, â= -2.
à  5, â= -2.
5, â= -2.
Âîïðîñ ¹ 73
How is located the straight Àõ+Âó+Ñ=0, if A=0
Parallel to the axis ÎÕ.
Coincides with the axis ÎÕ.
Date: 2015-12-11; view: 1609
| <== previous page | | | next page ==> |
| | | Parallel to the axis ÎÓ. |